首页 计算机专业课程笔记 计算机系统结构

# 第三章：流水线技术

# 3.1 流水线的基本概念

时 — 空图中横坐标代表时间，纵坐标代表流水线的各个阶段指令执行；
每个流水线段都要设置一个流水寄存器
各流水段的时间应尽量相等，流水线处理机的基本时钟周期等于时间最长的流水段的时间长度

流水线的分类：部件级（运算操作），处理器级（指令），系统级（程序）
静态流水线：在同一时间内，多功能流水线中的各段只能按同一种功能的连接方式工作
动态流水线：在同一时间内，多功能流水线中的各段可以按照不同的方式连接，同时执行多种功能
线性流水线：流水线的各段串行连接，没有反馈回路
非线性流水线：流水线中除了有串行的连接外，还有反馈回路
一条非线性流水线可以对应有很多张预约表，表示一种工作方式
顺序，乱序流水线，按照输出任务是否有序分类

# 3.2 流水线性能指标

吞吐率：在单位时间内流水线所完成的任务数量或输出结果的数量，TP=nTTP=\frac{n}{T}
各段时间不等（分别为 δti\delta t_i，分段mm）的流水线的实际吞吐率为：

TP=nΣi=1mΔti+(n−1)max(Δt1,...,Δtm)TP=\frac{n}{\Sigma_{i=1}^{m} \Delta t_i + (n-1)max(\Delta t_1, ..., \Delta t_m)}

最大吞吐率：

TPmax=1max(Δt1,...,Δtm)TP_{max}=\frac{1}{max(\Delta t_1, ..., \Delta t_m)}

解决流水线瓶颈问题的常用方法：细分瓶颈段，重复设置瓶颈段（使瓶颈段可以同时执行多个任务）

加速比：不使用流水线与使用流水线所用的时间之比

S=nΣi=1mΔtiΣi=1mΔti+(n−1)max(Δt1,...,Δtm)S=\frac{n\Sigma_{i=1}^{m}\Delta t_i}{\Sigma_{i=1}^{m} \Delta t_i + (n-1)max(\Delta t_1, ..., \Delta t_m)}

效率：在时空图上，nn 个任务占用的时空区（块）与 mm 个功能段总的时空区（块）之比
假定功能段的权值相等，则

E=nΣi=1mΔtim[Σi=1mΔti+(n−1)max(Δt1,...,Δtm)]E=\frac{n\Sigma_{i=1}^{m}\Delta t_i}{m[\Sigma_{i=1}^{m} \Delta t_i + (n-1)max(\Delta t_1, ..., \Delta t_m)]}

否则，设每一段（纵轴）权值为αi\alpha_i，Σi=1mαi=m\Sigma_{i=1}^{m}\alpha_i=m：

E=nΣi=1mαiΔtiΣi=1mαi[Σi=1mΔti+(n−1)max(Δt1,...,Δtm)]E=\frac{n\Sigma_{i=1}^{m}\alpha_i \Delta t_i}{\Sigma_{i=1}^{m}\alpha_i[\Sigma_{i=1}^{m} \Delta t_i + (n-1)max(\Delta t_1, ..., \Delta t_m)]}

# 3.3 非线性流水线的调度

预约表：横向（向右）是时间（一般用时钟周期表示），纵向（向下）是流水线的段。如果在第nn 个时钟周期使用第kk 段，则在第kk 行和第nn 列的交叉处的格子里有一个 ×
禁止启动距离：引起非线性流水线冲突的启动距离称为禁止启动距离
启动距离：向一条非线性流水线的输入端顺序输入两个任务之间的时间间隔称为启动距离（等待时间）
启动循环：不发生冲突的启动距离一般是一个循环数列，称为非线性流水线的启动循环，记作（1，7），代表如 X2 在 X1 后一个时间间隔启动，X3 在 X2 后 7 个时间间隔启动

  • 步骤一：由预约表得到禁止集合
  • 步骤二：由禁止集合得到冲突向量
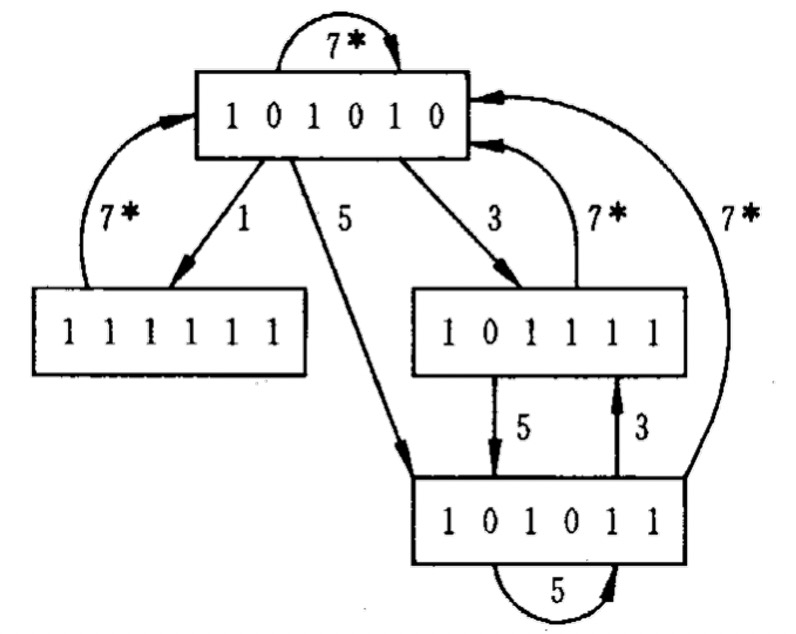
  • 步骤三：由冲突向量构造调度流水线的状态图
  • 步骤四：在状态图中找出可用启动距离（从初始状态出发，能构成一种间隔拍数呈周期性重复的方案），并根据简单循环（各种冲突向量只经过一次）计算平均启动距离
  • 步骤五：找出平均启动距离最小的启动循环或恒定循环
    禁止集合：将一条非线性流水线的所有各功能段禁止启动距离组合在一起形成的数列
    冲突向量：mm 位的二进制数表示（mm 位禁止集合最大值），禁止集合中的相应位置11
    状态图：将冲突向量CC 作为初始冲突向量送入一个mm 位逻辑右移移位器，移位mm 次，移出00 则与初始向量作按位或运算

    找出所有在状态图中各种冲突向量只经过一次的简单循环，计算平均距离，取最小值的循环

最小平均启动距离的限制范围：下限是预约表中任意一行里 × 的最多个数，上限是冲突向量中 1 的个数再加上 1
因此，理想最小平均启动距离（MAL）等于预约表任一行中 “×” 的最多个数，理想最小启动循环是恒定循环

采用预留算法来调度非线性流水线，可以达到最优调度；核心思想是插入 非计算延迟段 ，可以体现在流水线中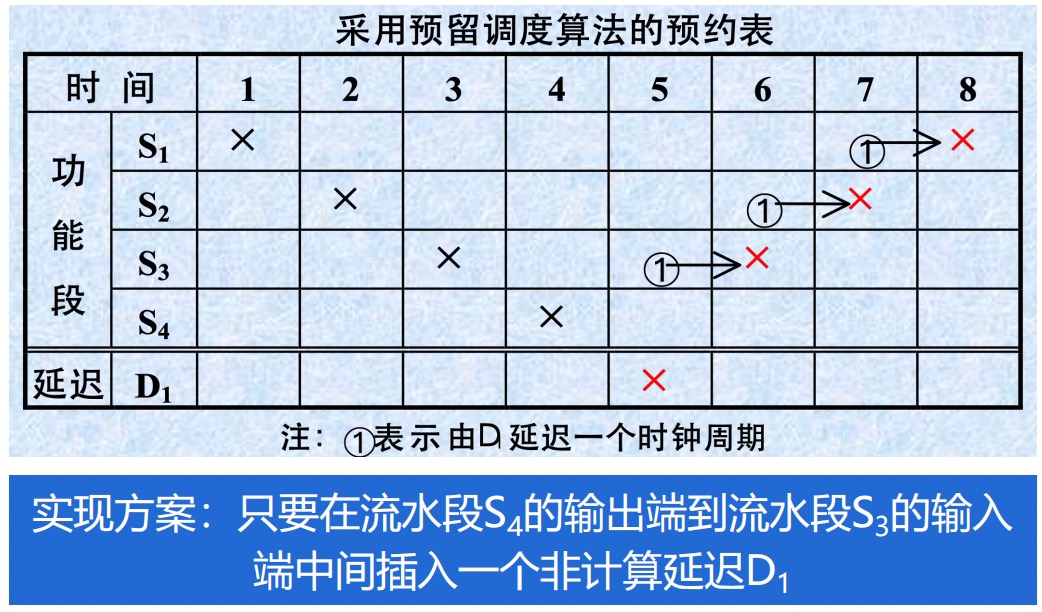

实现最优调度的目标是使 “瓶颈” 流水段处于忙碌状态，没有空闲周期

启动间隔集合：从启动循环CC 推导出各个起始之间所有可能的时间间隔集合Gc(modp)G_c(mod\ p)，pp 为循环周期
在禁止启动集合为FF，启动间隔集合GcG_c 的流水线中，当且仅当F(modp)∩Gc(modp)=∅F(mod\ p) \cap G_c(mod\ p)=\emptyset 时，周期为pp 和启动间隔集合GcG_c 的启动循环CC 才是允许（安全）的。

# 3.4 相关与冲突

指令相关有三种类型：数据相关（真相关，RAW），名相关（输出相关 WAW、反相关 WAR、是一种假相关），控制相关（改变 PC）
流水线冲突：结构冲突，数据冲突，控制冲突
通过定向技术（即数据旁路）减少数据冲突引起的停顿
延迟分支：从逻辑上延长分支指令的执行时间。把延迟分支看成是由原来的分支指令和若干个延迟槽构成，不管分支是否成功，都要按顺序执行延迟槽中的指令；延迟槽由编译器调度完成
延迟指令的调度：从前调度，从目标处调度，从失败处调度

# 3.5 流水线的实现

流水线最佳段数的选择：最大吞吐量 / 流水线价格