# 绪论
序列的有穷性至今无法证明。
计算机不会产生绝对随机的理想随机数,只会产生伪随机数。
图灵机模型, 随机存取模型,假设寄存器能够任意直接访问,每一操作仅仅需要常数时间。
:,i.e. 是上界。
:,i.e. 是下界。
:,i.e. 与 同阶。

# 常用级数:算术、幂、几何、对数等
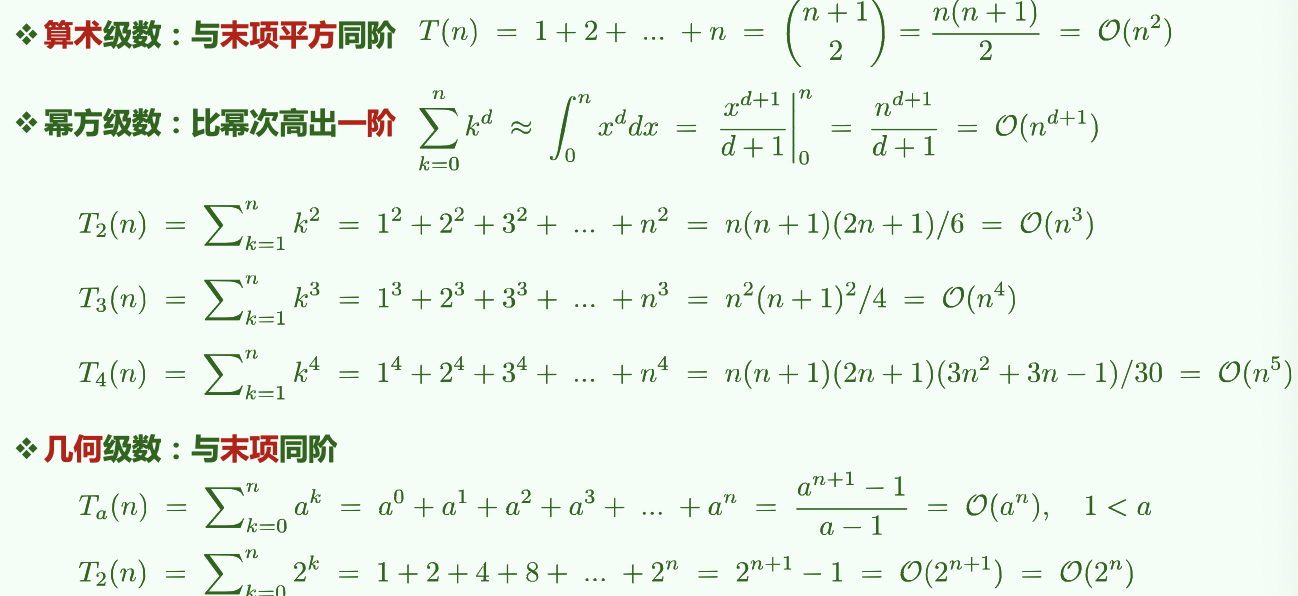
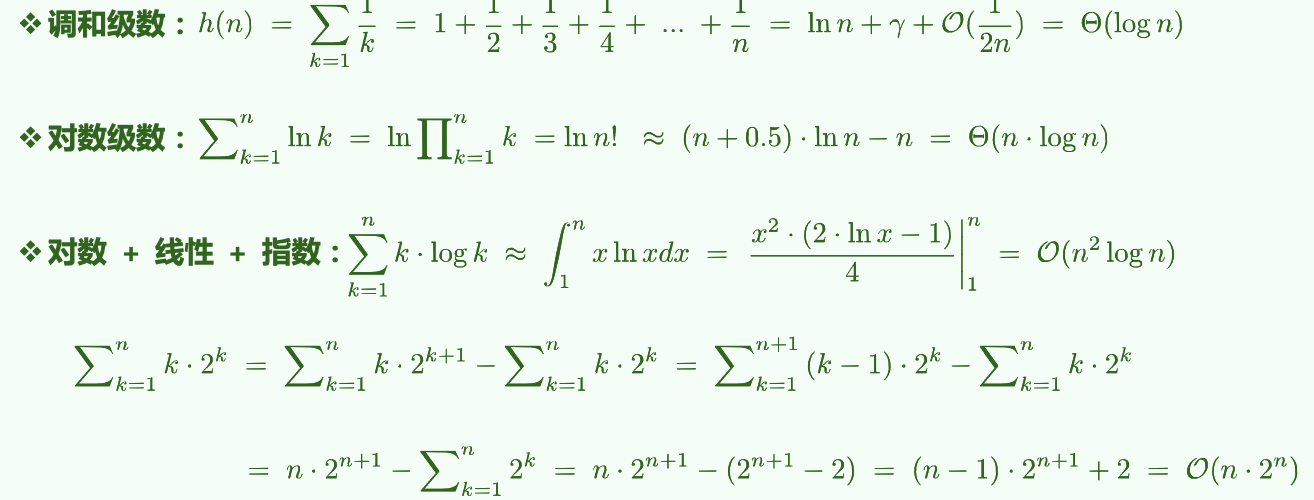
# 不常见的分数级数

减而治之:使用递归跟踪(列出所有实例)或递推方程求解。
# Master Thm.
不同分治对应的复杂度:
分治通常递推形式:
即:原问题被分为 a 个规模均为 的子任务;(每一层)任务的划分、解的合并耗时。
( 要小于 O 中的表达式,因为 O 是其上界)
e.g. kd-search:
e.g. Binary search:
e.g. Merge Sort:
e.g. quickSelect:
# 例子:总和最大区段
分而治之:,总复杂度。
方法:计算左右区间最大总和,以及跨越切分线区间的前缀最大和后缀最大之和,取其最大值。
减而治之:总和最大区段要么是最短总和非正后缀的后缀,要么与其无交集,因此非正后缀可以反复剪除,复杂度。
# 动态规划
递归低效采取记忆化解决,动态规划与递归方向相反。
例子:最长公共子序列,复杂度
# 向量
向量是数组的抽象与泛化,各元素与 的秩一一对应。
容量递增策略:每次追加固定容量,总体耗时,均摊成本为。
容量加倍策略:每次发生溢出扩容一倍,总体耗时,均摊成本为。
平均分析:根据各种操作出现的概率将成本加权平均。割裂了相关性和连贯性,不够准确
分摊分析:连续实施足够多次操作,将总体成本分摊至单次。更为精确实际
有序向量的唯一化高效算法:每次搜索不同的项统一移动到头部区域内。
# 有序向量的二分查找
中点为轴点,两次比较的平均查找长度为。
斐波那契查找,,平均查找长度。
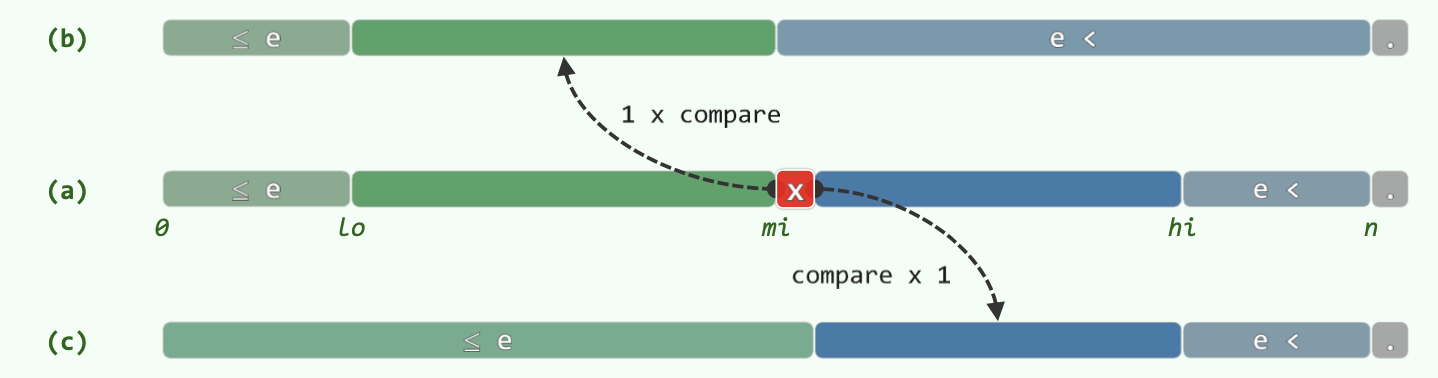
改进思路一:左右分支代价不平衡的问题,改为仅作一次关键码比较,最后判断 s[low] == e 是否成立。
改进思路二:总返回不大于 e 的最大元素秩。
BinarySearch(data, e, lo, hi): // [lo, hi)
{
while (lo < hi)
{
median = (lo + hi) / 2
if (e < data[median])
hi = mi // [lo, mi)
else // (data[median] <= e)
lo = mi + 1 // [mi + 1, hi) = (mi, hi)
} // break when (lo == hi)
return (lo - 1)
}
以下陈述在算法执行全过程中总是对的:
A[lo - 1]是已知的小于等于 e 的数(A[0] ~ A[lo - 1])中最大的A[hi]是已知的大于 e 的数(A[hi] ~ A[n])中最小的
据此,可以以初始状态成立为基,进行数学归纳;按照循环中的两个分支分别归纳,发现无论哪个分支,两个条件仍然是对的。因此最后 A[lo - 1] 是已知的小于等于 e 的数中最大的。
# 插值查找
根据 猜测轴点 的位置,大致呈线性趋势增长的序列。
平均每经过一次比较,待查找区间宽度缩至,复杂度降低到,优势不明显。
实际可行的方法:首先插值缩小范围,然后用二分查找,最后数据项极小时用顺序查找。
# 冒泡排序
改进一:提前终止。可能发生某一次扫描发现无需交换,代表已然有序,此时可以终止。
改进二:跳跃版。虽然红色 部分未有序,但是它的某个后缀可能有序。维护一个 last 值,初始值为 lo ,每次发现逆序对 (i,i+1) 时,就令 last=i 。如此从前向后扫描一趟之后, last 记录的就是最后一个逆序对的位置。如此,逆序对只可能存在于 [lo, last) 中。特殊地,如果整趟扫描没有发现逆序对,则 last 仍然为 lo 值。之后的 hi = last 操作会使 hi == lo ,从而终止循环,在这种情况下相当于提前终止。

时间效率最好,最坏,严格不等关系才交换(相等不交换)就是稳定的。
# 归并排序
最坏,也适用于列表,以及磁带之类的设备。
出现重复元素时通过左侧的向量中的元素优先归并可以保证稳定性,易于并行。
但是并非就地,需要对等规模的辅助空间,最好情况也需要 时间。
# 列表
循位置访问,拥有哨兵节点 header 和 tailer 。
有序列表的去重可以直接调用删除。查找时只能有 算法。
# 选择排序
前 个元素已经有序;考查第 个位置;遍历 往后的所有元素,选择最小的与当前第 个位置的元素交换,交换拥有两种模式。
。遇到重复元素需要选定靠后位置优先,如果用 模式,不稳定!如果用区间平移模式,稳定。
采用 模式,每迭代一步,最值 都会脱离原来的循环节,自成一个循环节。因此无需交换的情况对应最初循环节的个数,最大为,期望为。
# 插入排序
因为列表搜索只能顺序搜索,复杂度。而使用向量的话插入复杂度很高,反而更慢。
前 个元素已经有序;考查第 个元素,从第 个元素向前遍历,寻找合适位置,将其插入其中,使得有序区间成为前 个元素。
复杂度分析:插入位置共 个,每个位置等概率,比较次数分别为。
# 逆序对
逆序对总数。
对于冒泡排序,交换操作次数等于输入序列逆序对的总数。对于插入排序,关键码比较次数为逆序对数。
归并排序统计逆序对数。左右两部分的有序序列合并时,假设下标 i 的数在左边,下标 j 的数在右边,对于右边的 j ,统计左边比它大的元素个数 f(j) ,在区间 之间,即 f(j) = mid-i+1 ,合并完所有的序列时即可得出答案,即 f(j) 之和便是答案。
# 栈
递归函数的空间复杂度主要取决于最大递归深度(递归树的深度)而不是递归实例总数。
尾递归不难转化为迭代。通常消除递归只是在常数意义上优化空间。
栈混洗顺序数:
禁形:不存在 模式的序列。通过直接模拟可以得到 的判断栈混洗方法。
逆波兰表达式:后缀表达式
# 队列
双栈当队:入队在 R 栈,出队时将 R 栈全部 pop() 到 F 栈,再出栈。
势能分析法:
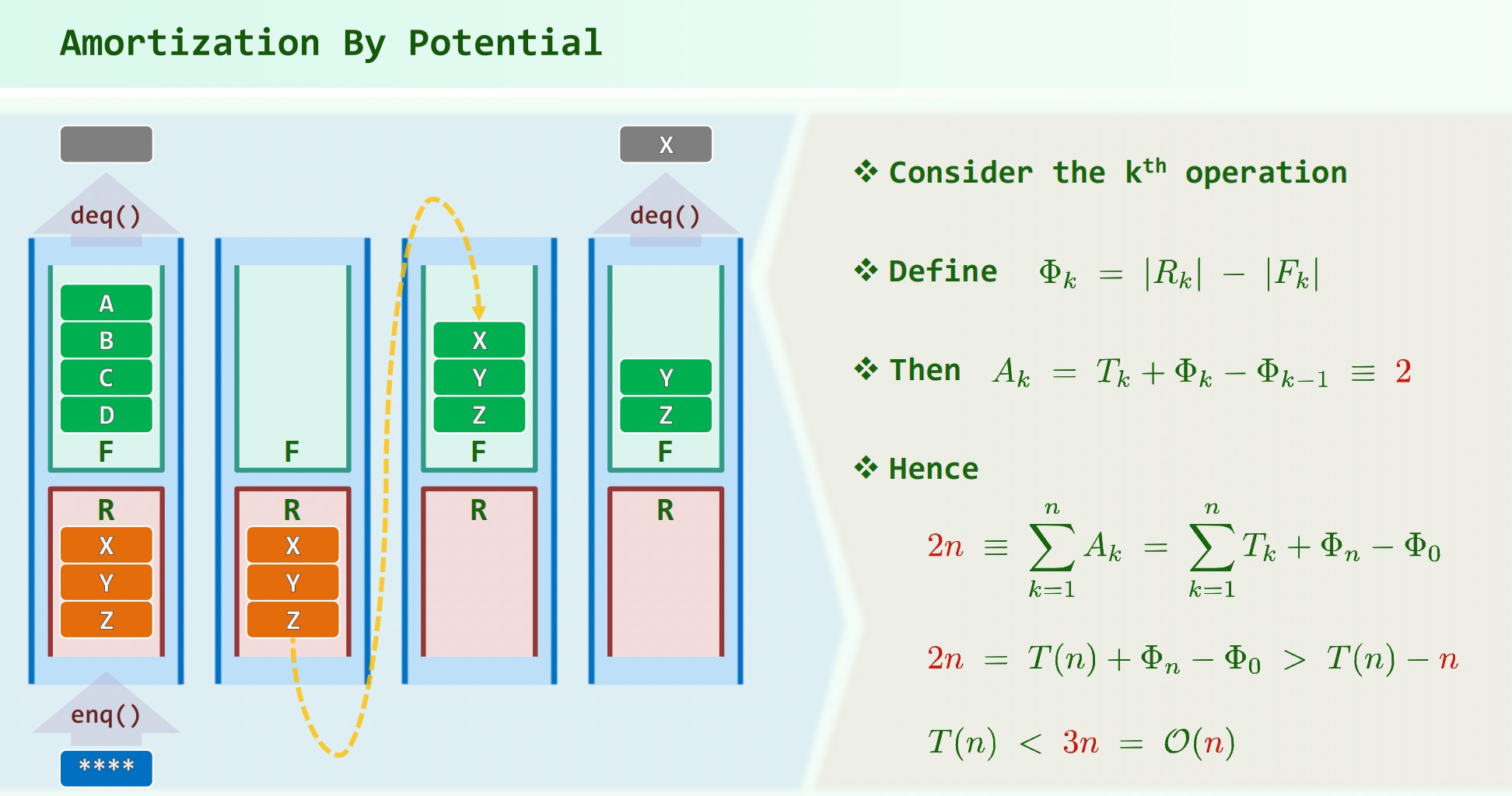
# Steap
两个栈 P 和 S,P 中每个元素都是 S 中对应后缀的最大者。
入栈 S 直接 push ,P 与栈顶比较后将 max(e, P.top()) 入栈;
出栈返回 S.pop() , getmax() 返回 P.pop() 。
# Queap
两个队 P 和 Q,P 中每个元素都是 Q 中对应后缀的最大者。
入队 Q 直接 enqueue() ,P 在 enqueue() 之后从队尾开始搜索比 小的项全部赋值;
出队与 getmax 同上。
# 实例:直方图内最大矩形
对于每一个横坐标 要确定的是在它左侧比 H[r] 低连续区间最小的左端点 和在它右侧比 H[r] 低连续区间最大的右端点。
离线算法:借助栈前后各搜索一遍,每次 入栈前弹出栈顶开始所有比 高的元素,如果栈空则,否则为 1 + S.top() ,然后 入栈。
在线算法:
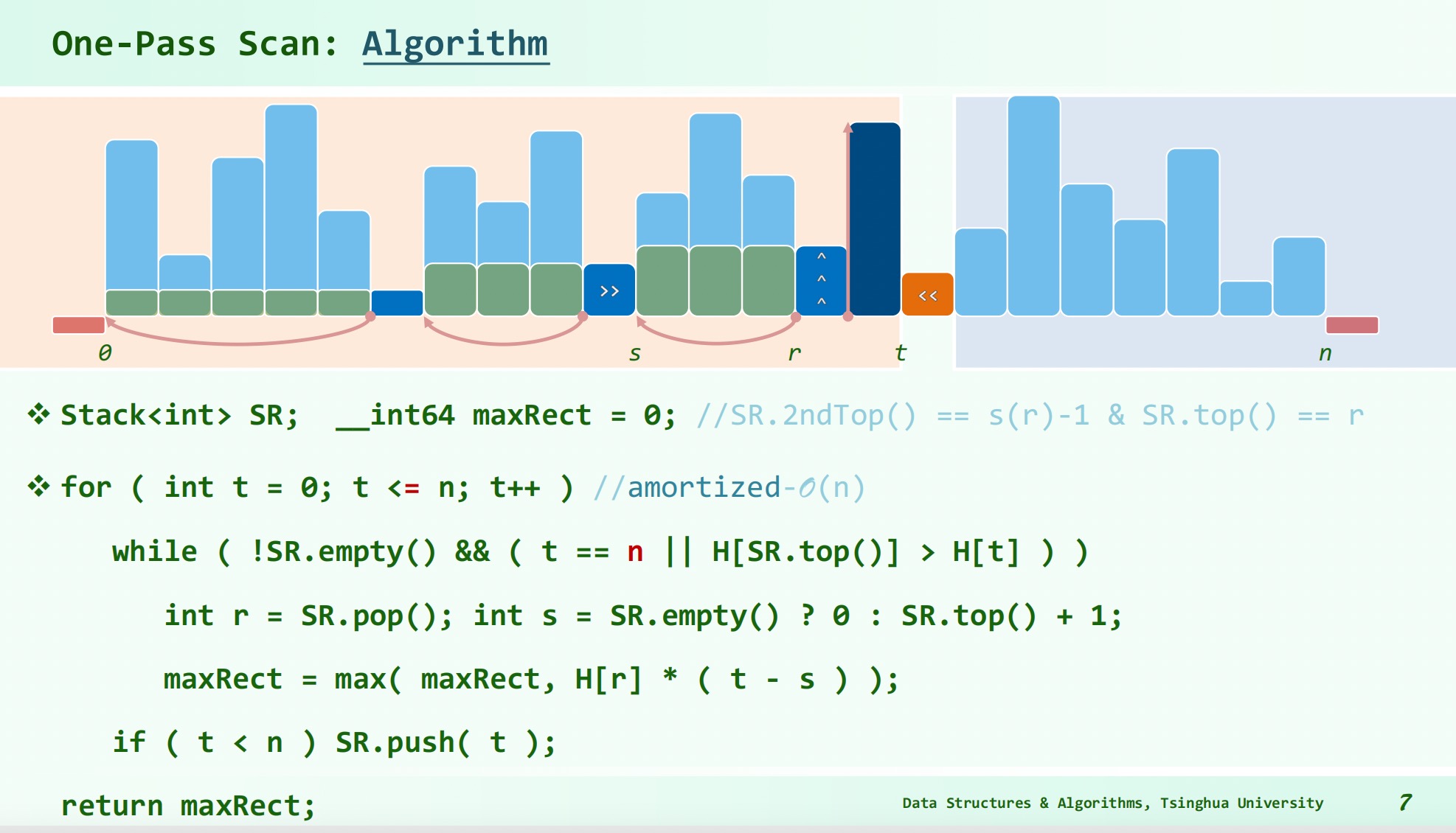
# 树
树是极小连通图,极大无环图。
深度,到根节点的路径的边的数目。。
高度:树 T 的所有节点深度的最大值。只有根的树:;空树:。
度:孩子的个数。
# 二叉树
孩子可以左右区分,隐含了有序条件。
有根且有序的多叉树可以用长子 - 兄弟表示法表示为二叉树。
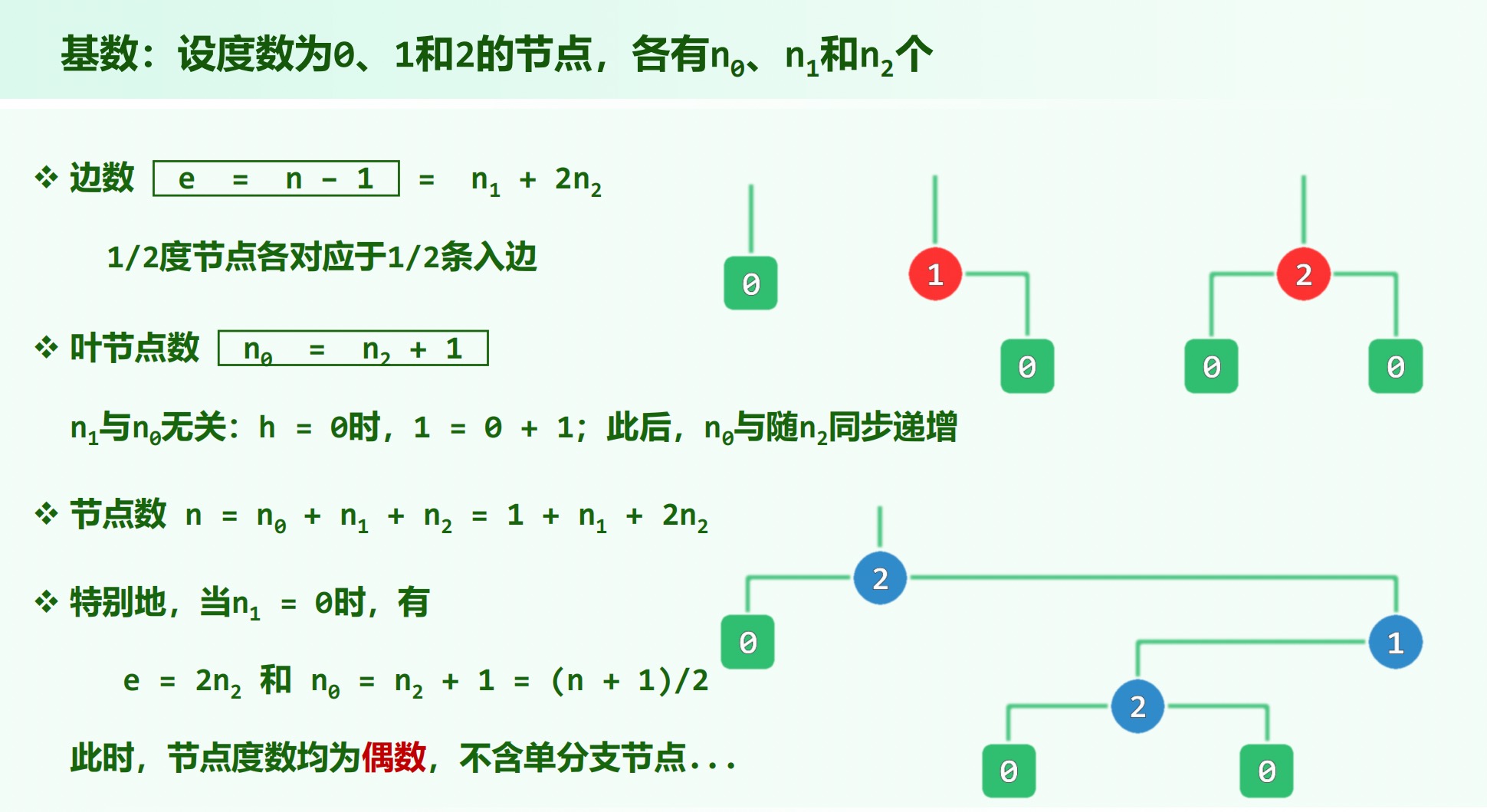
满树:
真二叉树:引入 个外部节点,使原有节点度数统一为,不改变全树复杂度,简化红黑树等的描述。
# 二叉树遍历
迭代版先序遍历:自上而下访问左侧的 “藤” 上节点,再借助栈自下而上遍历右子树。
迭代版中序遍历:沿着左侧 “藤”,通过栈自下而上先访问藤上的节点,再遍历其右子树。
不借助辅助栈:设置标志位 backtrack ,每当抵达一个节点,判断此前是否刚做过一次自下而上的回溯,若不是则沿左子树优先访问,否则意味着当前节点的左子树遍历完毕,即可 visit 该节点再深入右子树。
但是需要调用 succ() 来实现回溯(同时设置 backtrack = 1 ),时间效率倒退。
后继 succ() :右孩子的最小左孩子(先朝右下移动,再不断朝左下移动),或是让该节点在其左子树中的最低祖先(不断朝左上移动,最后一步朝右上)。
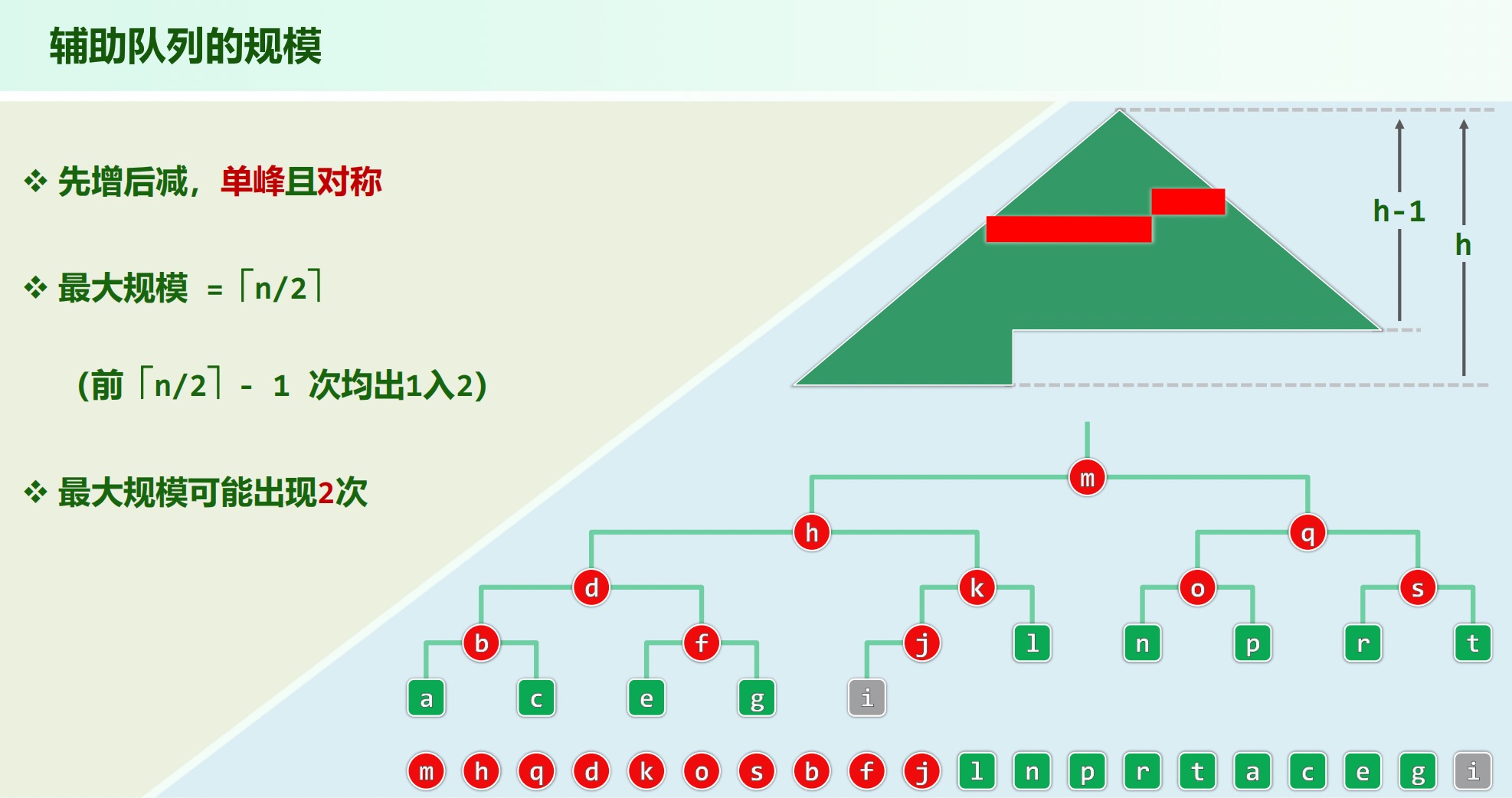
层次遍历:借助队列的广度优先搜索。
完全二叉树:叶子节点仅限于最低两层,最底层的叶子均居于次底层叶子左侧(满二叉树 + 最底层左侧叶子)。
性质:叶子节点数 = 内部节点数(存在度为 1 的节点)或 叶子节点数 = 内部节点数 + 1(所有节点度为 2 )
由先序序列和后序序列不能唯一确定一棵二叉树,因无法确定左右子树两部分。
反例:任何结点只有左子树的二叉树和任何结点只有右子树的二叉树,其前序序列相同,后序序列相同,但却是两棵不同的二叉树。
增强序列:
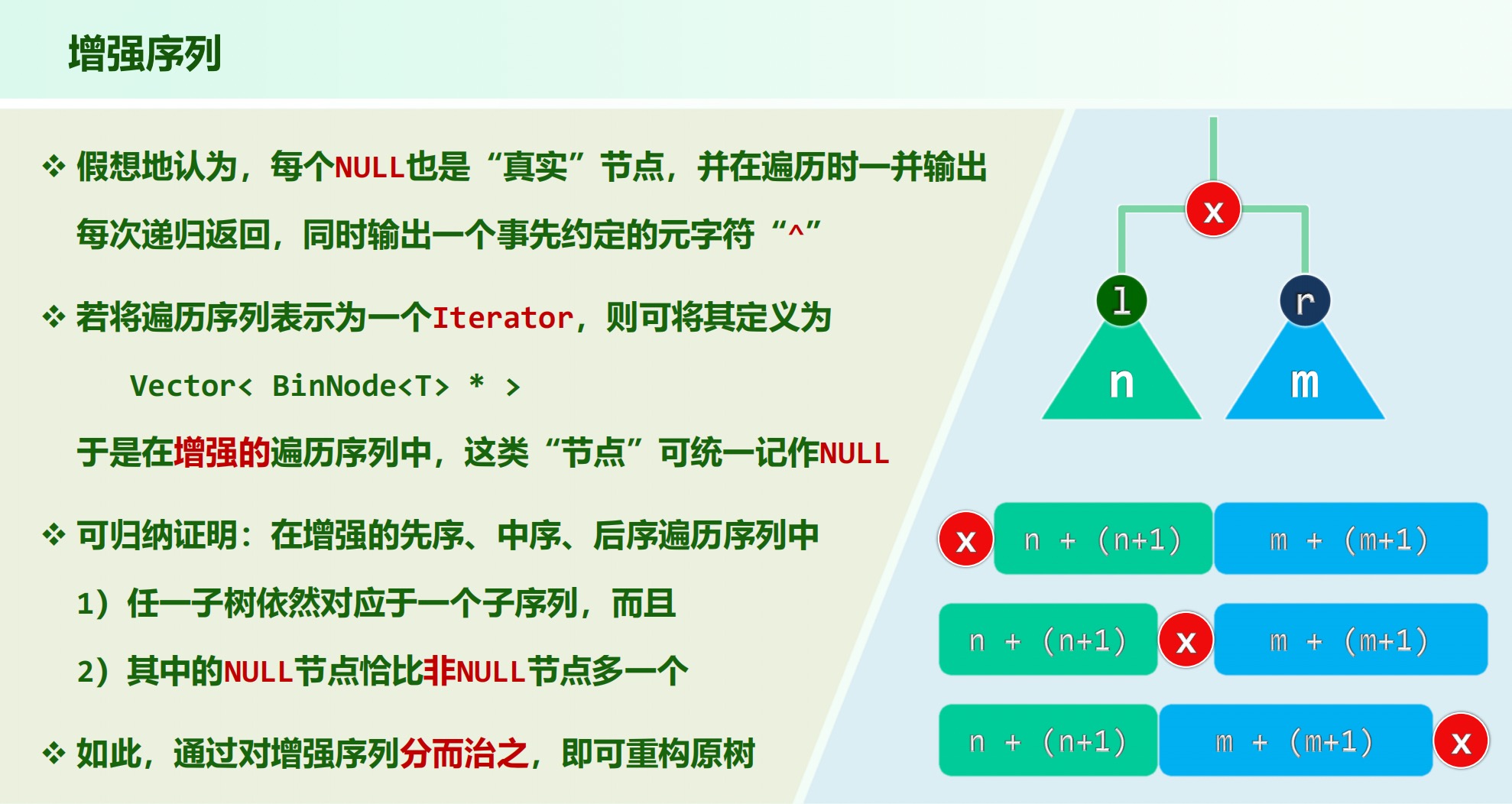
# Huffman 树
最优编码树,平均编码长度最小(不带权)。性质:叶子只能出现在倒数两层以内。
最优带权编码树,即 树,叶节点平均带权深度最小。
特征:每一个内部节点都有两个孩子,节点度数为偶(真二叉树);不唯一性(通过要求左子树频率更低也无法消除);层次性(频率最低的都是最底层的兄弟)
编码算法使用列表或向量为 复杂度,使用优先队列为。
# 二叉搜索树
n 个互异节点随机组成的二叉树,记共有 棵不同的情况,则:
。
若各种 BST 等概率出现,则平均高度。
若 n 个互异词条按各种排列次序(各种排列等概率)插入,平均高度。因为不同的插入序列可能对应相同的二叉树拓扑结构。
插入操作先调用 search 查找失败找到新节点的父亲,插入的节点必为叶节点,插入后更新高度。
如果节点拥有的孩子不超过 1,将其替换为他的子树(或直接删除)。否则,找到其(x)直接后继(w),交换两者;让 w 的子树代替 x,完成删除。
查找,插入,删除操作均线性正比于树的高度。
理想平衡: 个节点构成的二叉树高度为,表现为完全树或满树(叶子节点只能出现在最低两层)。
渐进平衡:高度渐进地不超过。
渐进平衡的二叉搜索树称为平衡二叉搜索树(BBST)。
单次动态修改操作后,至多 处局部不满足平衡条件,通过 甚至 次旋转 可以恢复平衡。
# AVL 树
平衡因子 = 左子树高度 - 右子树高度,绝对值在 1 以内。
高度为 的 AVL 树,至少包含 个节点。
# 插入
从祖父开始,每个节点都有可能失衡。
从插入节点(叶子)的 parent(hot) 开始向上走,维护高度,直到第一个失衡节点 g;通过 tallerChild(tallerChild(g)) 确定 p,v,然后用一次 3+4 重构重平衡;重平衡后的节点及其祖先高度必然复原,故可直接退出循环。
由于高度复原性质,整个 insert 最多 1 次 3+4 重构(2 次旋转)。
。
# 删除
用 BST 的删除,删除,记录 hot 。
从 hot 向上,一旦发现 失衡,通过 tallerChild(tallerChild(g)) 确定,,然后用一次 3+4 重构重平衡;重平衡后的节点高度可能降低,
失衡可能传播,需要一直向上,执行多次 3+4 重构。
。
# 3+4 重构
各种不平衡的情况都可以按照 “中序”,顺着最长的分支考察祖孙三代统一平衡。
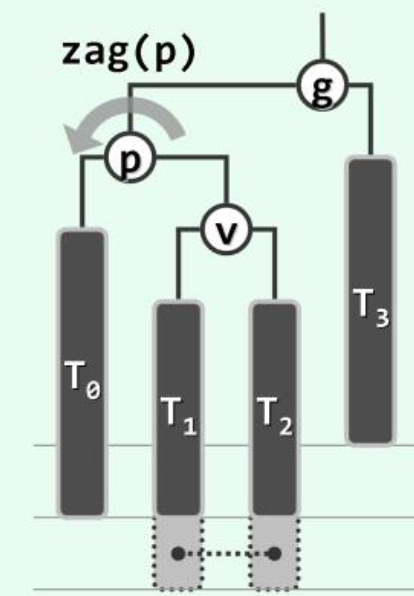

# 性能
存储空间,最坏情况下的复杂度均为。但是实际复杂度由于旋转成本较高,单次动态调整后全树拓扑结构的变化量可能高达,与理论值有差距。
# k-D 树
一维区间查找,计数耗时,即二分查找;枚举耗时,最坏情况达。
缺点:不能推广到二维甚至高维平面。
二维区间查找算法,对空间每一个点预处理,表示其左下方含有点的个数,时间和空间复杂度达到,然后用容斥原理求解。虽然单次查找时间不超过,但整体性能很差。
# 创建
记录点信息和分割维度信息,每次递归更新一个维度,取该维度的中点作为分割线。
每个节点对应平面的一个 Canonical Subset ,它其中的元素是这个节点子树中的所有点。同一深度的点对应子区域之和是整个平面。
# 查询
设从节点 v 开始搜索,搜索区间是 R。
kdSearch(v, R):
if v is leaf:
if v in R:
report(v)
if v->lChild in R:
reportSubtree(v->lChild)
else if v->lChild have intersection with R:
kdSearch(v->lChild, R)
if v->rChild in R:
reportSubtree(v->lChild)
else if v->rChild have intersection with R:
kdSearch(v->rChild, R)
# 复杂度
空间复杂度
2-D 树时间复杂度分析:
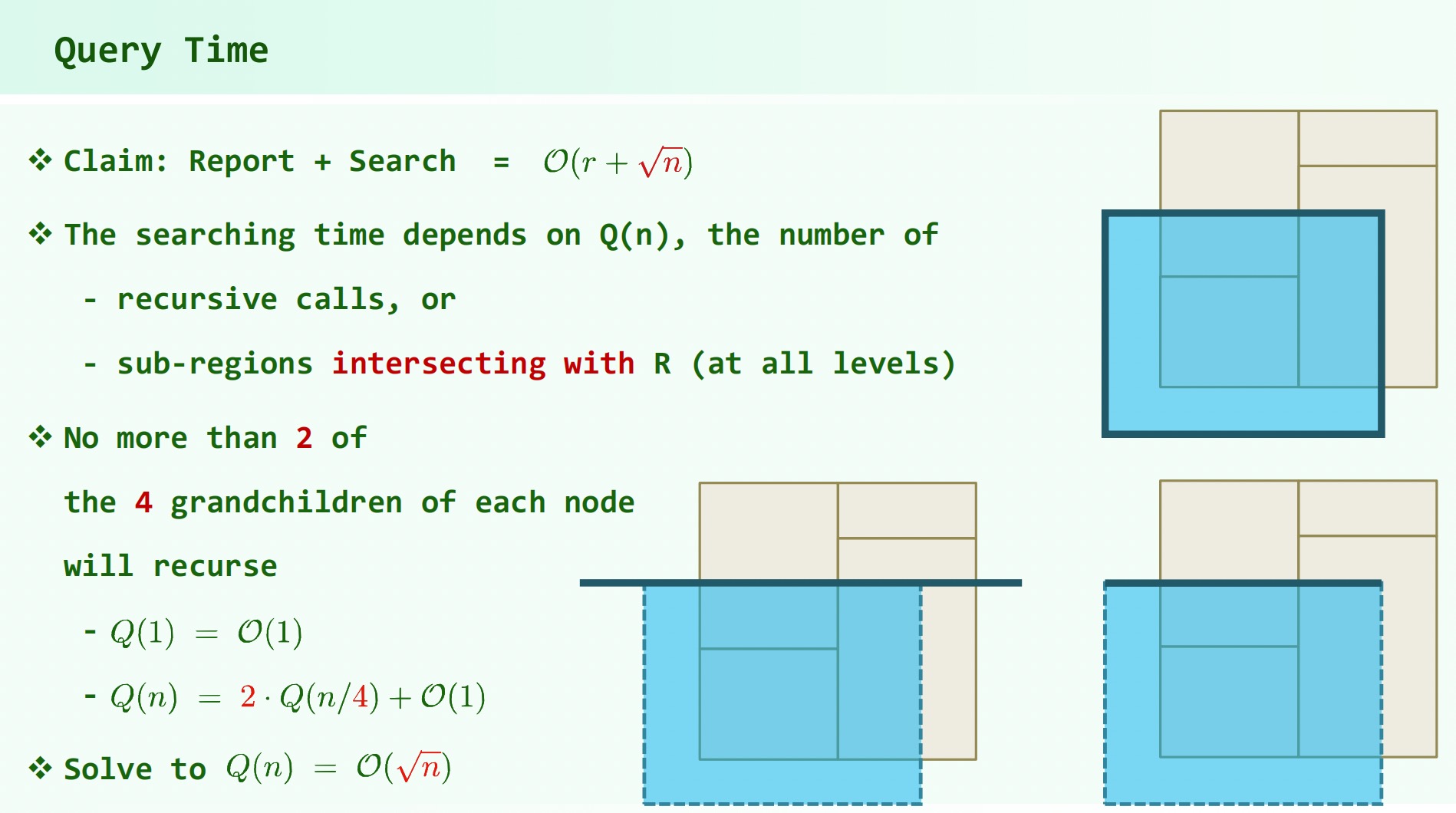
包含枚举复杂度:
拓展到高维( 维):
查询:
创建:
# 多层搜索树(MLST)
对于 x 维的 1-D 树每个节点对应的 Canonical Subset (即一个包含整个 y 轴的竖长条区间)中的所有点再构建 y 维的 1-D 树,即一棵 y - 树的 x - 树。
查询算法:首先根据 x 维的区间范围确定所有 Canonical Subsets ,即对两个端点搜索到叶子节点的路径。由于树高度为,这样的 Canonical Subsets 有 个。
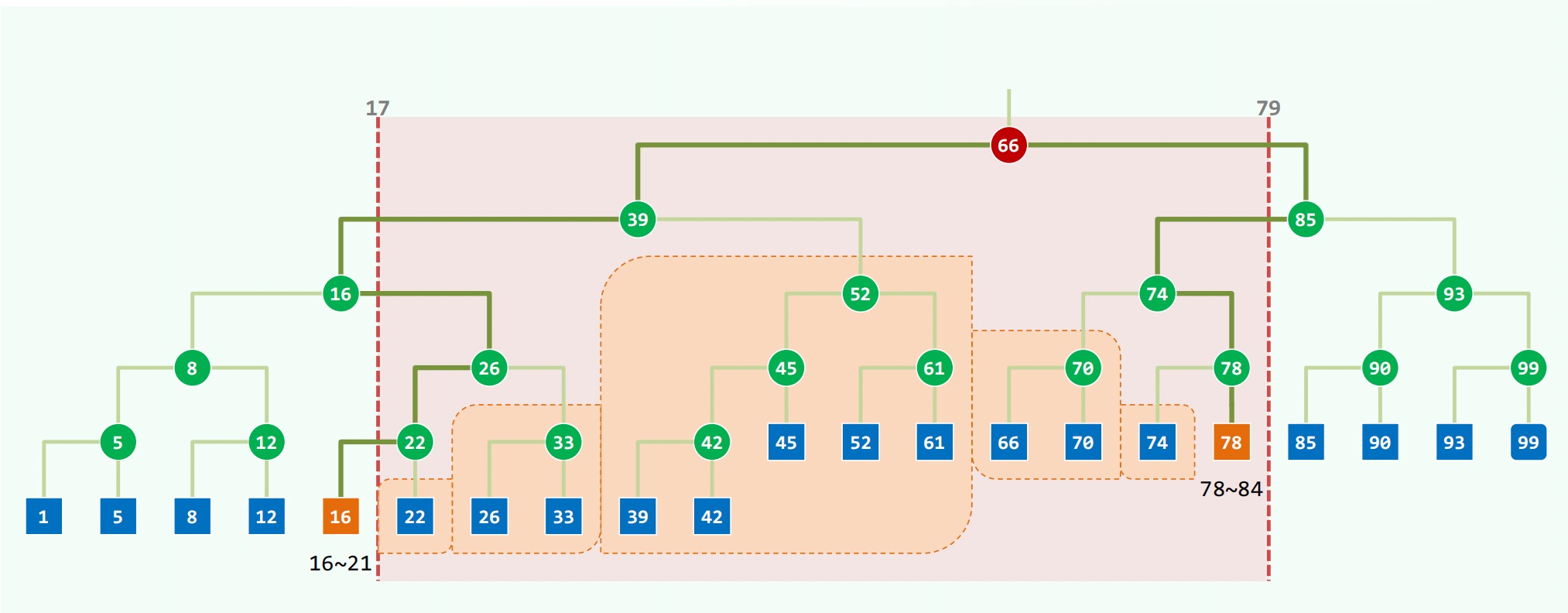
之后再对这些点对应的 y - 树进行类似的搜索操作,找出区间中涵盖的点。
建树复杂度,查询复杂度。由于每个输入点都存储在 个 y - 树中(对应从 x - 树叶子节点到根的路径上所有节点),空间复杂度。
推广到 d 维:空间复杂度,创建时间复杂度,查询复杂度。
# 区间树
问题:给定一个一维区间集合,求包含某个点的区间个数。
建树:给出所有区间的端点集合,,令 为 P 中端点的中点,所有区间分成三份, 为所有右端点在 左侧的区间集合, 为包含 的所有区间集合, 为所有左端点在 右侧的区间集合。令 和 为 的左右孩子。之后递归建树。
对于每个树节点保存了其对应的 和集合中的区间(按照左端点和右端点分别排序)。
查询: 为查询到的节点, 为问题中的那个目标点。

建树复杂度,主要就是排序算法;查询复杂度。空间复杂度。
# 线段树
将所有区间分割为单位区间并排序,每两(一)个单位区间合并为他们的父亲,在大多数情况下一个单位区间就是一个点(否则可以离散化近似处理)。
之后将每个区间插入线段树并标记, 代表节点对应的区间:
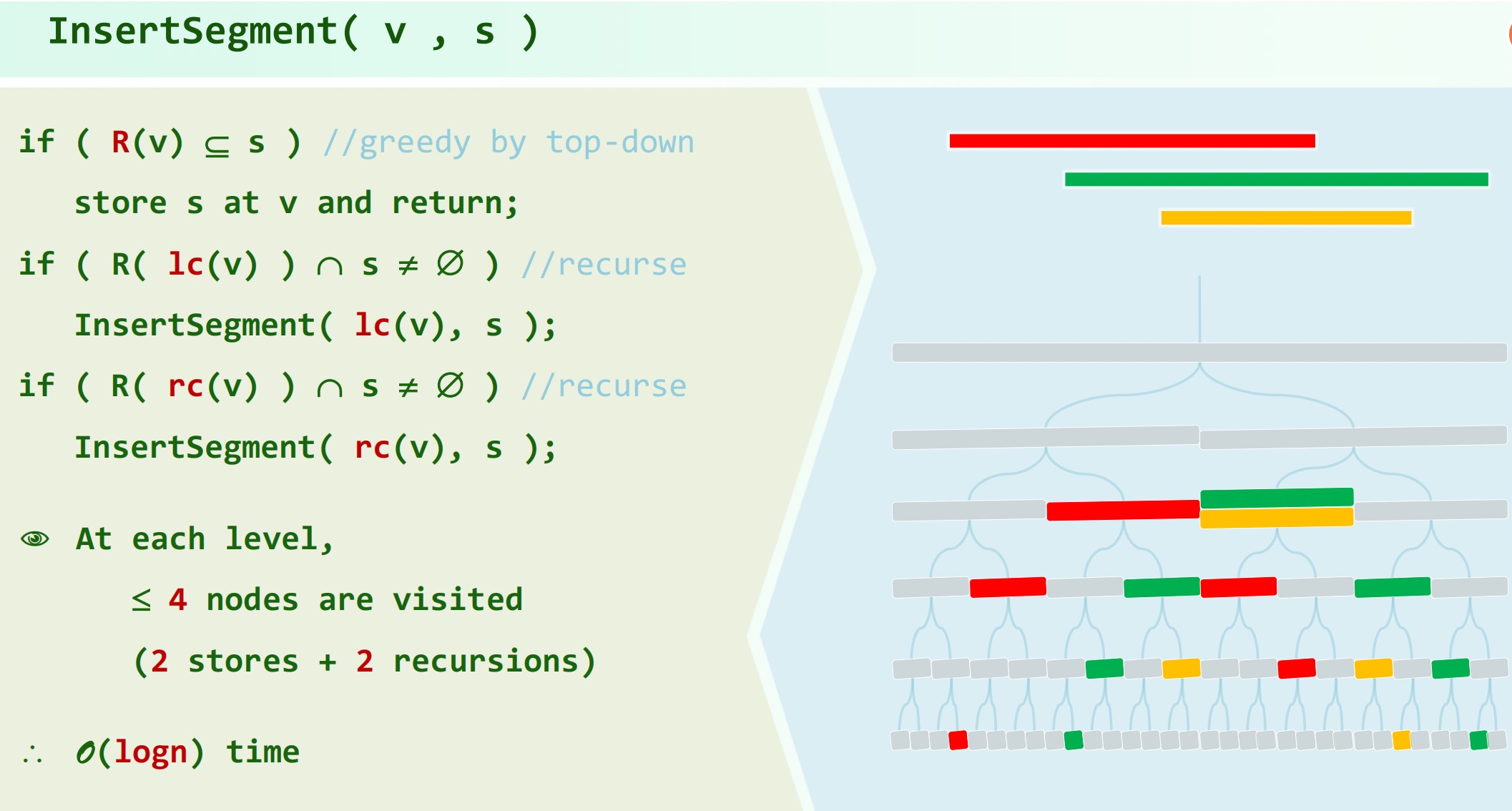
查询 时,设查询到节点,首先累计 所记录的区间,然后根据 是否在左右孩子中递推。
空间复杂度。查询 复杂度,建树复杂度。
# Splay 树
# 局部性
时间:刚刚访问过的节点极有可能很快被再次访问;
空间:下一次要访问的节点极有可能就在刚被访问过的节点的附近。
# Splay
单层伸展的局限性:最坏情况下(BST 退化为链表)伸展复杂度分摊。
双层旋转之 “顺向情况”(),在最坏情况下对应路径的长度减半,不会持续发生最坏情况:
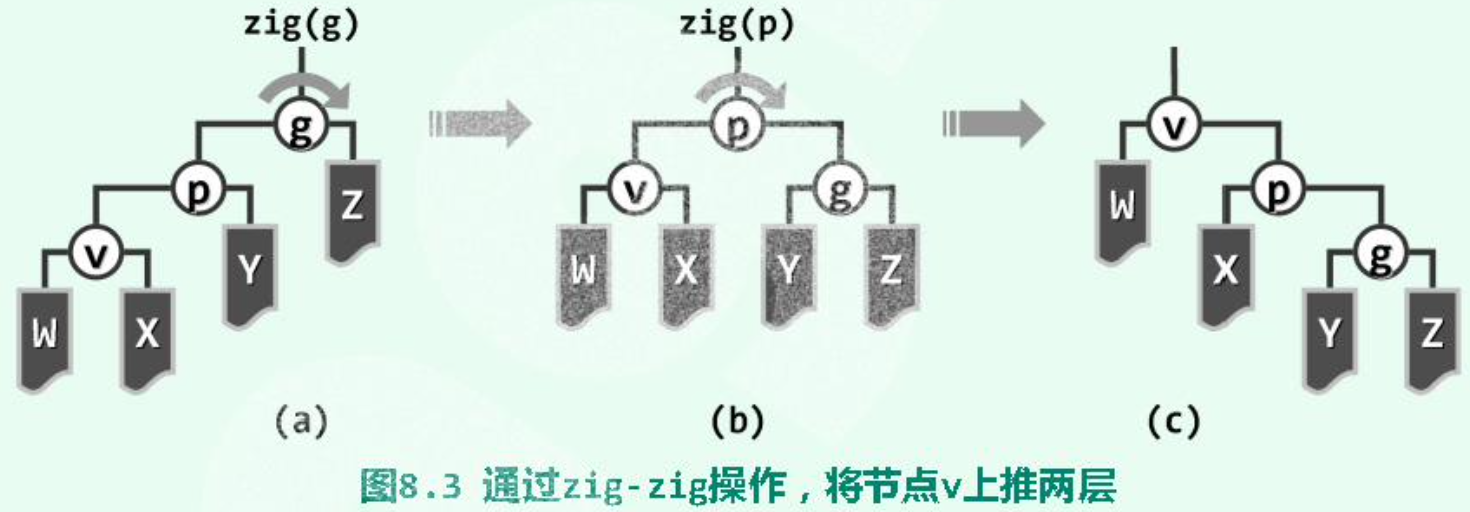
双层旋转之 “反向情况”(),该情况与单层伸展相同:
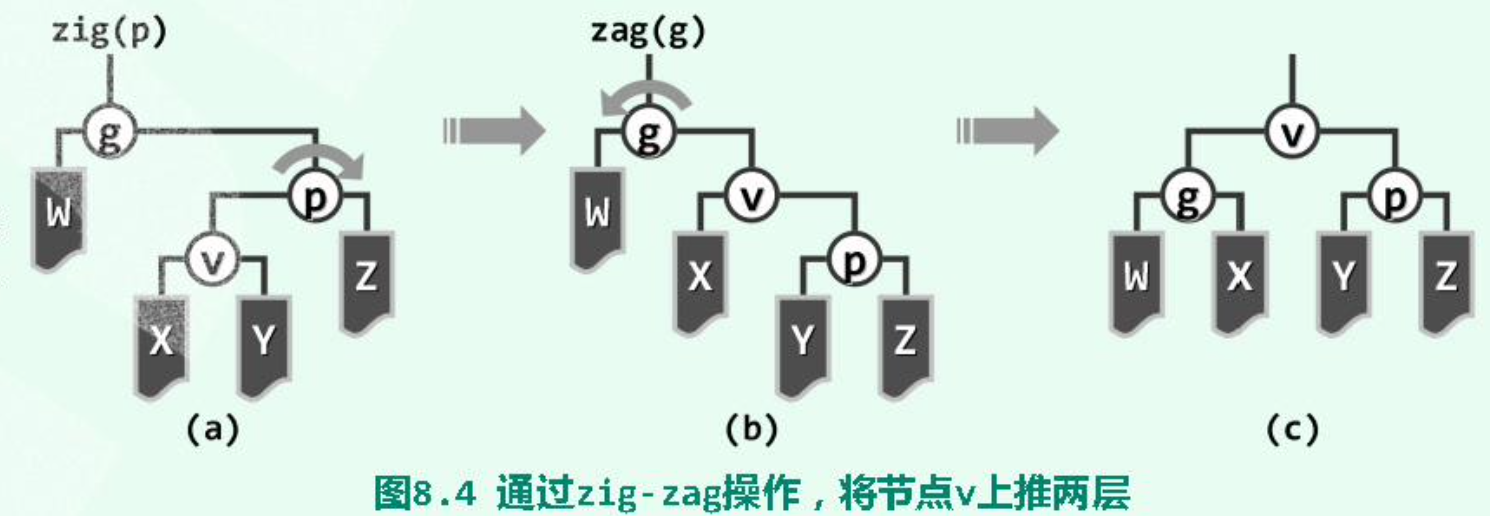
单层旋转:当待 至根的节点的 parent 为 root 时:
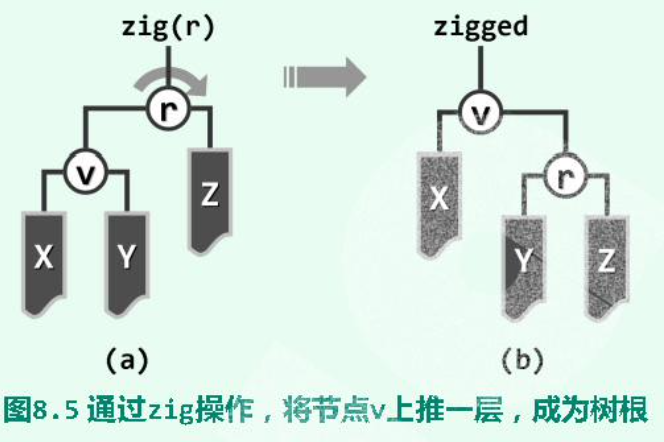
# 查找
为保证性能,无论成功与否,需将最后访问的节点旋转至 root。
search(value):
{
p = searchIn(root, value, hot)
root = splay(p ? p : hot)
return root
}
(hot 记录了 search 中最后到达的节点)
改变了树的拓扑结构,不再属于静态操作。
# 插入
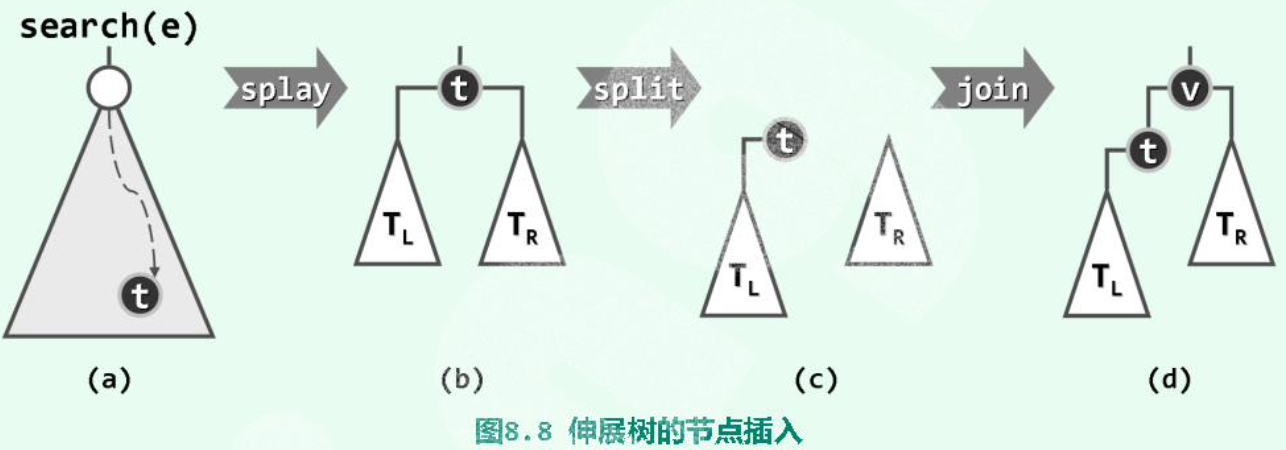
- 调用 的
search算法,待插入节点不在树中,查找失败。 - 但 “待插入位置” 的父节点
hot,记为,已经被旋转至根。 - 根据 与要插入的数值的大小关系,将 及其子树与 重组为新的树。最后新插入的 作为
root。图中对应 的情况。
Corner Case: 当 <u> 连续插入有序序列 </u > 时,Splay 会呈现链状。当然,不一定完全有序,如:3,2,1,4,5,6,7,…… 也可以形成链状。
# 删除
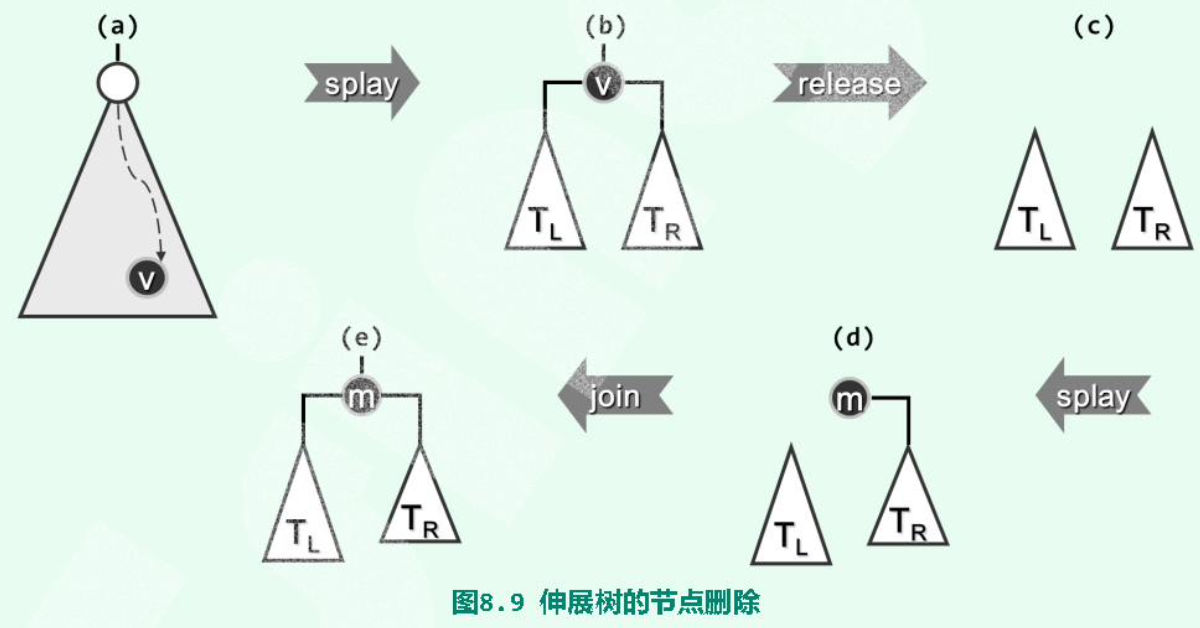
- 查找(search)待删除值 v,v 会被 Splay 至 root。
- 删除 v,剩下它的两个子树、。
- 为空,则 就是余树。
- 在 中查找 v;这一查找必定失败,但会将 中的最小值 m,即 v 的直接后继,旋转至子树 的根。
- 由于 m 是 v 的直接后继,因此 中 m 的左子树必为空。直接将 作为 m 的左子树。完成。
# 分摊复杂度分析
定义任何时刻伸展树 的势能,其中 为以 为根的子树大小。
越平衡 / 倾侧的树势能越小 / 大。
对于单链树,。
对于满树,。
对于伸展树的 次连续访问(仅考察 search() ),记第 次访问,因为,所有式子累加得。
若能证明,即可得。
显然有等式,这是因为单个节点的子树规模变化不至于超过。
考虑三种不同的伸展操作:
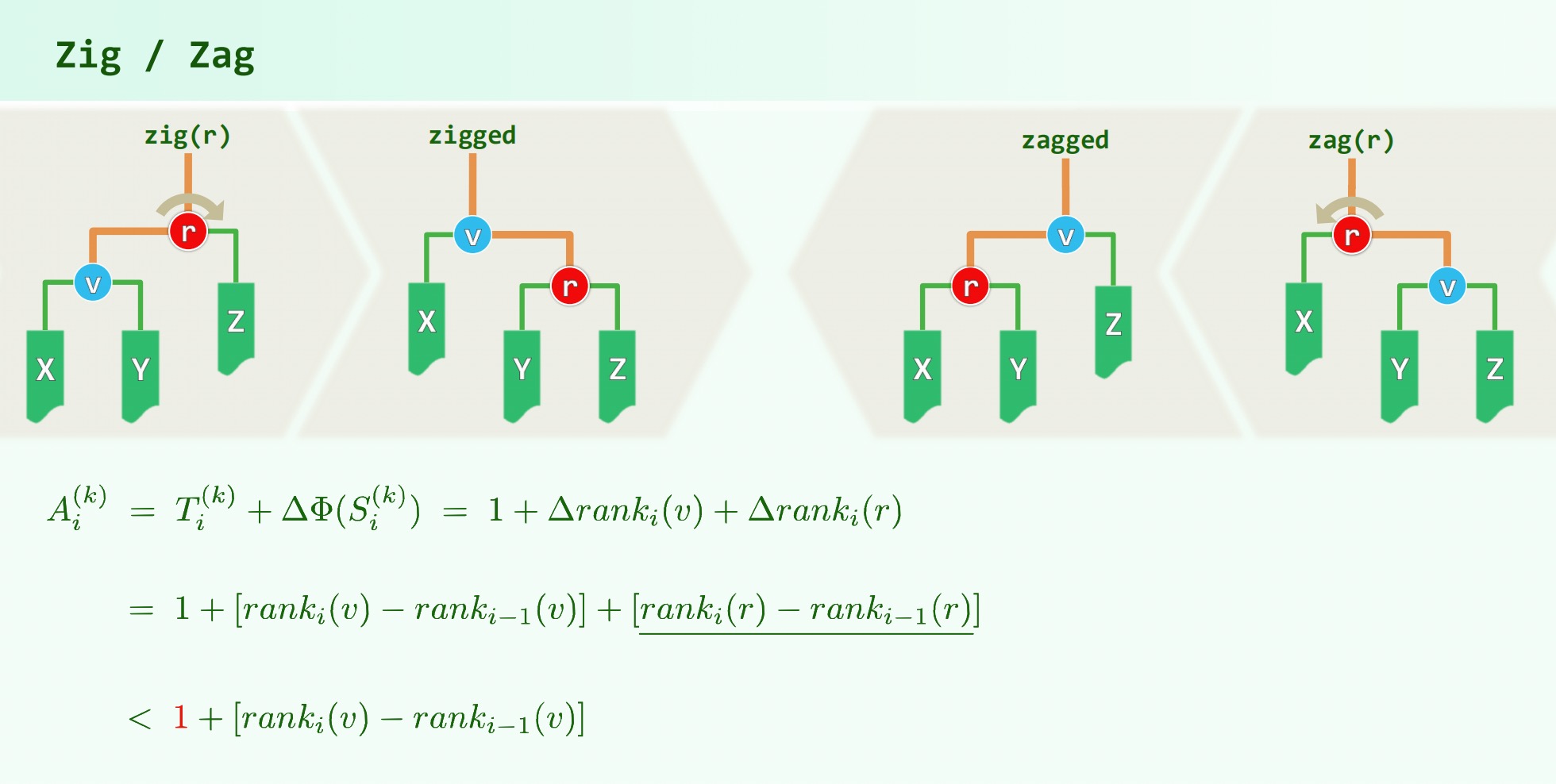
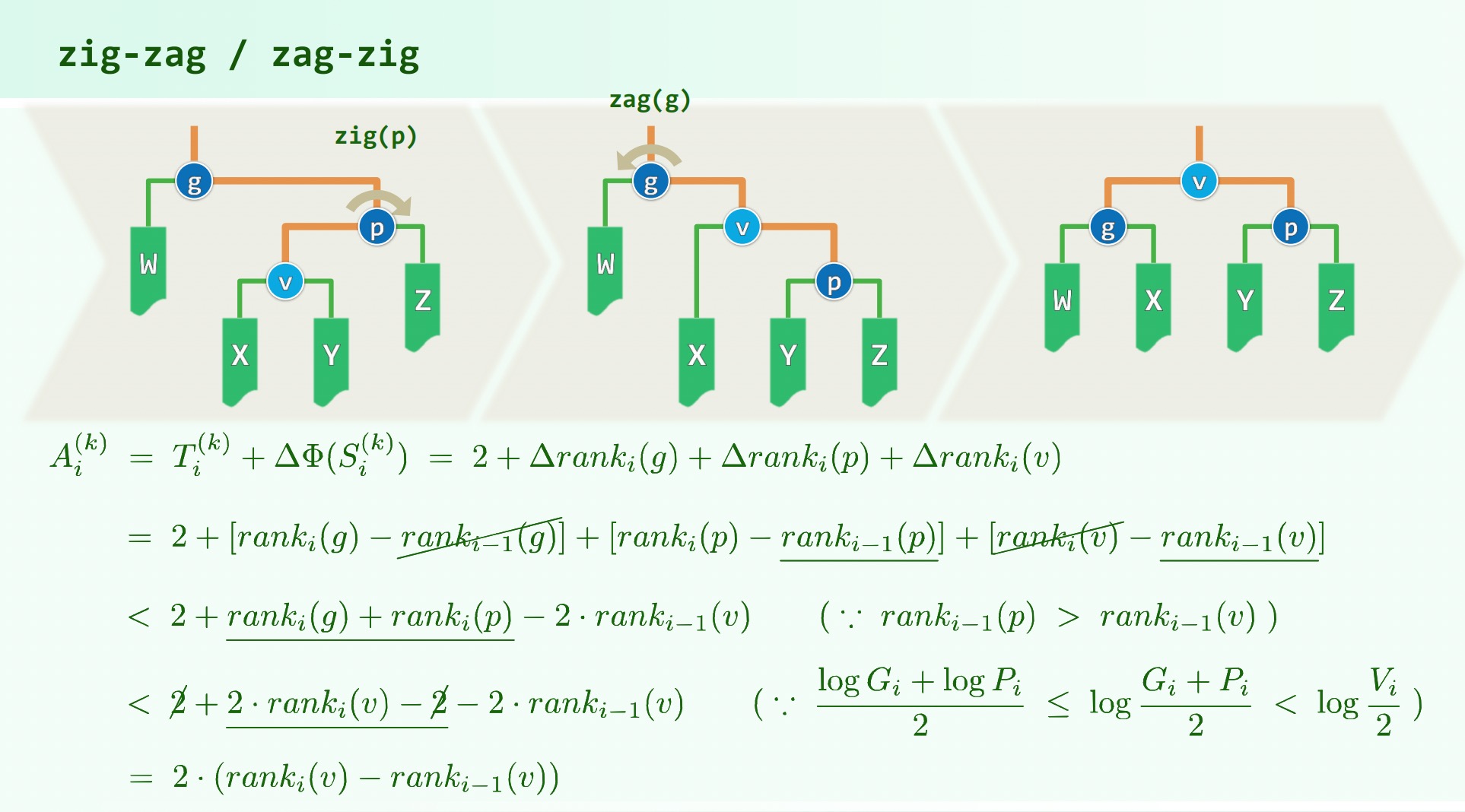
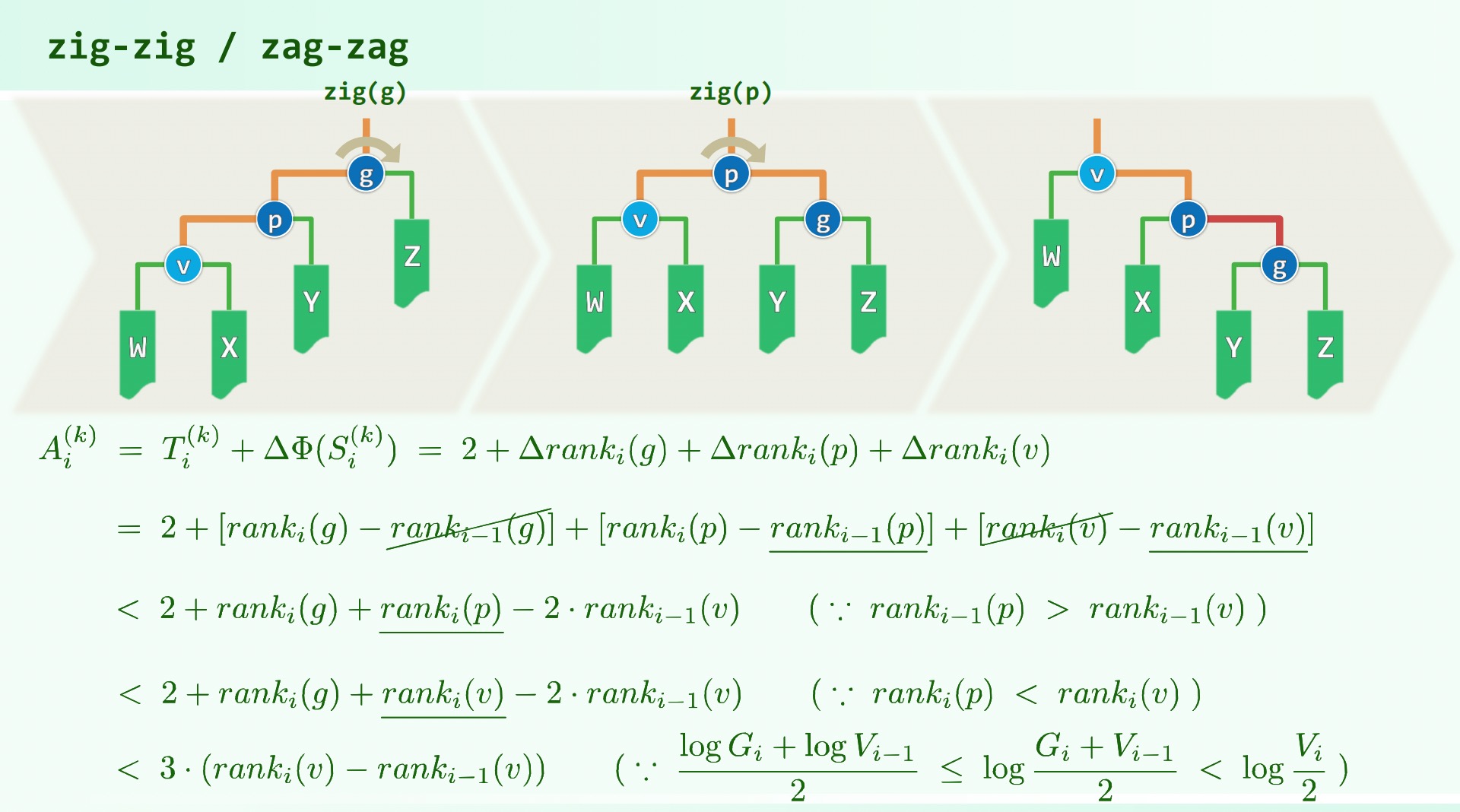
因此 都不至超过, 等式成立,时间复杂度。
# B Tree
# 现实
存储器容量增长的速度远小于应用问题规模的增长速度;存储器容量越大,访问速度越满;现实的存储系统由不同类型的存储器级联而成,不同等级的存储器访问速度差异悬殊,因此常用的数据因复制到更高层,更小的存储器中,找不到再向更低层的存储器索取。
算法的实际运行时间主要取决于相邻存储级别之间数据传输 IO 的速度和次数。
批量访问:在外存读取 1B 与读写 1KB 几乎一样快。
# 循环移动
使用 辅助空间将数组 A[0,n) 向左循环移动 个单元。
蛮力算法:反复以 1 为间距循环左移,。
迭代版算法: shift(A, n, s, k) 从 开始,间隔为 依次替换左移,使得 个同余类中的一个就位;列举所有同余类即可。内层复杂度,总复杂度。
倒置版算法:。
reverse(A, k); //O(3k/2) | |
reverse(A + k, A - k); //O(3(n-k)/2) | |
reverse(A, n); //O(3n/2) |
# 定义
m 阶 B-Tree,每个节点有 个 key, 个分支。()
需满足。(除了根节点分支数要求不少于 2 其他节点不能少于 的一半)
也称 。
外部节点的深度统一相等,记为树高,叶子节点的深度统一为。
每个节点两个 Vector ,分别存储 key ,指针。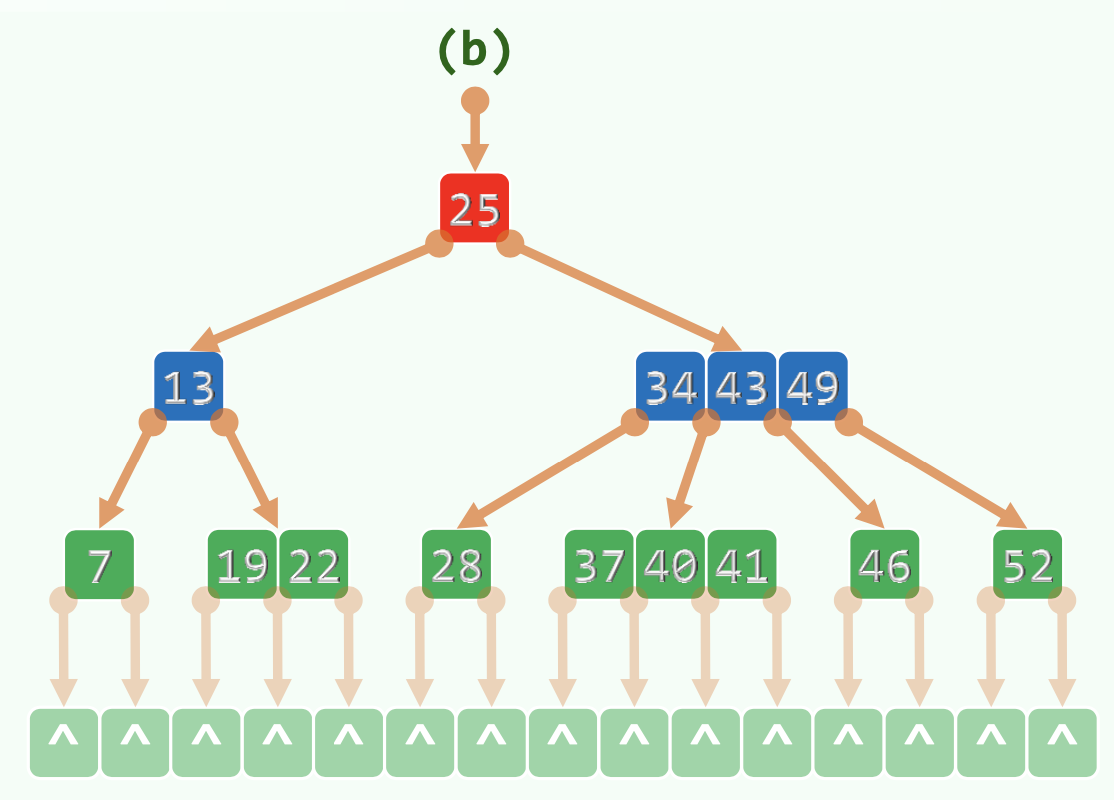
某 node 中,两 key 之间的下级指针指向的 node 中的 key 介于两 key 之间。
# 树高
最大树高:内部节点尽可能瘦,高度为 的所有节点,式子中的 表示根至少有 个子节点,之后所有子节点都至少有 个子节点。
对于外部节点数量为,代入得,得。比 的 具有优势。
最小树高:内部节点尽可能胖,,,得。
当 时,最大树高较 为,最小树高为。
# 查找
每一层内部顺序查找。但因为顺序局部访问很快,时间可以忽略。(外存批量访问的优点)
当找不到时,转入下一层查找。在当层节点向量中的 search() 返回最大的小于 的秩为,则搜索它的第 个孩子。(秩从 开始)
运行时间主要取决于 IO 次数,即向下一层访问的次数,复杂度。 为 key 的个数。
# 插入
先插入:
寻找,确认其不存在,寻找过程中记录了
hot(查找失败的最后一个node的parent)。在
hot里搜索,由有序性确定插入位置,插入,创建空的子树指针。
视情况做分裂。
# 上溢与 split
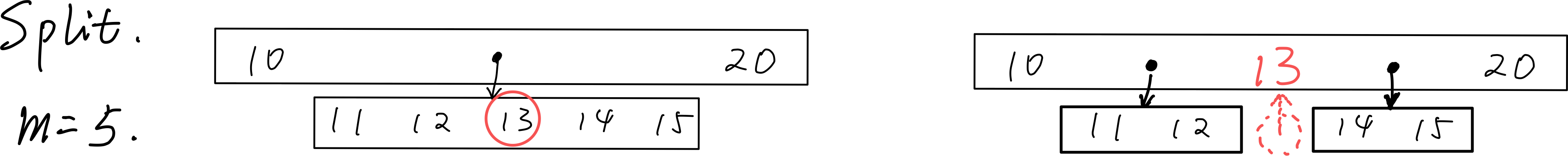
- 上溢节点恰好有 个
key。 - 找到上溢节点中居中的
key,以之为界将节点一分为二。 - 将居中的
key提升至原节点的parent中,以分裂后的两个节点为左右孩子。 - 左右孩子关键码数不小于,符合要求。
上溢传递:最多传到根。如果根满了,就上溢 作为新的根,它仅有两个分支,这是 B - 树增高的唯一可能。
显然上溢传递次数是有界的。
。
# 删除
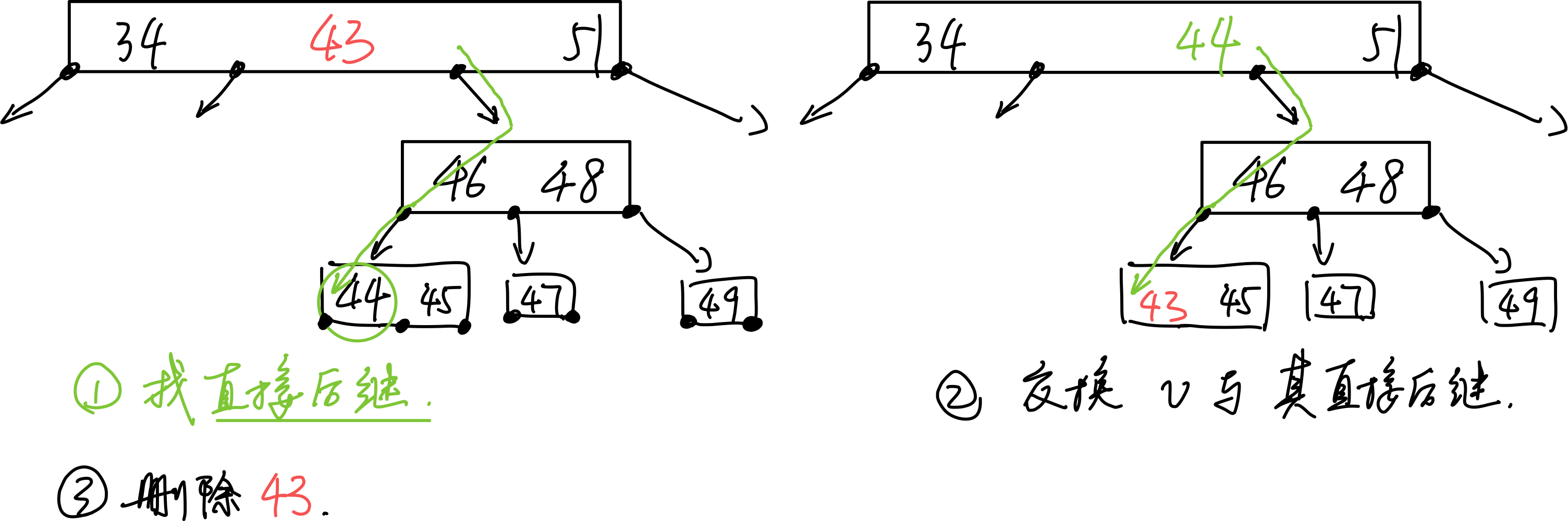
- 找直接后继的数:对于非叶节点需先找直接后继节点:先往右下一次,然后一路向左,直到叶节点,与其交换。
- 删除交换后的,需要删除的,已经在叶节点中的数。
删除后需要处理下溢。
# 下溢
下溢节点恰好有 个 key 。
分情况:
(1)(Rotate )左兄弟(同 parent )存在,且其 key 个数不小于:
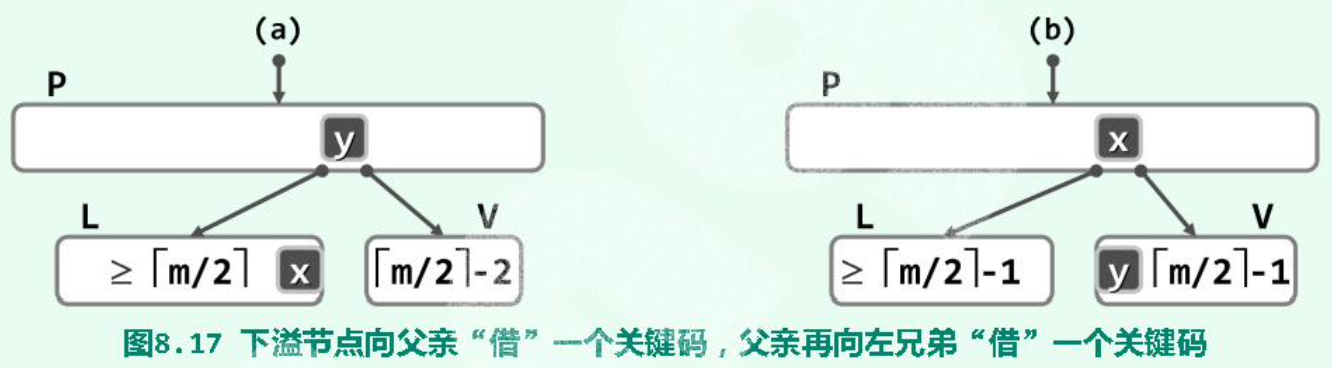
(2)(Rotate )右兄弟(同 parent )存在,且其 key 个数不小于:
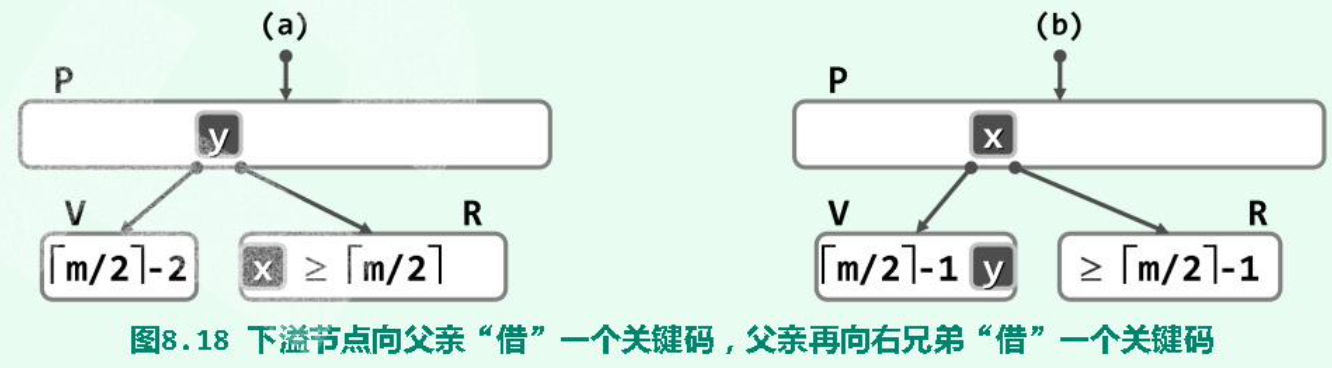
(3)(Combine )L 或 R 不存在(不可能同时不存在,因为一个 node 至少两个分支),或 key 的个数已达下限不能再给出:
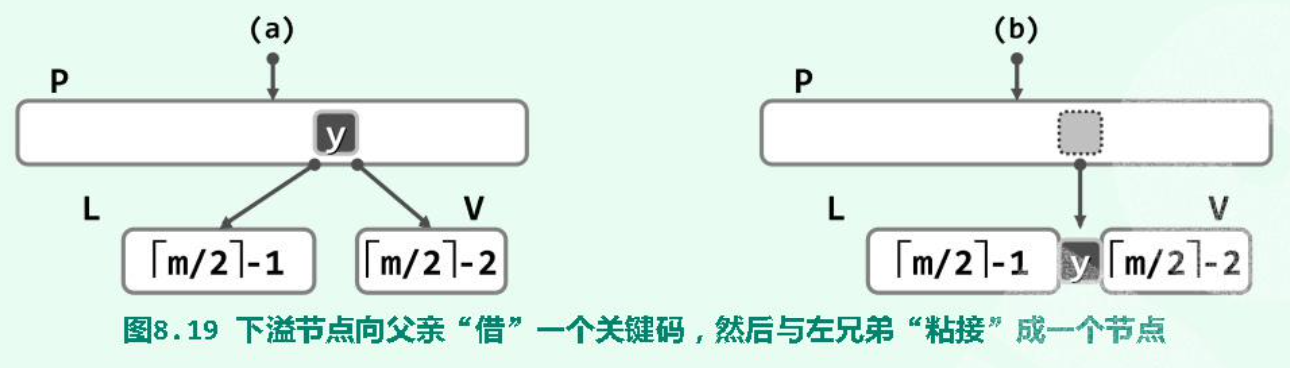
合并出来的节点一定满足 key 个数的范围条件。
父节点 P 少了一个 key ,可能下溢。因此这种情况的下溢会传递。如若导致根节点为空,则根节点的两个孩子合并后的节点成为新的根(一定只有两个孩子)。
# 红黑树
# 动机
并发性:结构变化处加锁,要确保 insert/remove 时的变化不超过。
持久性:支持对历史版本的访问。
压缩存储:大量共享,少量更新,每个版本新增复杂度仅仅为。
# 定义
- 为所有有需要的节点引入 n+1 个外部节点,使得所有节点的左右孩子非空。
- 树根
root:黑色 - 外部节点:黑色
- 其余节点:若为红,则只能有黑孩子(红之子,之父必为黑)
- 外部节点向上到根:途中黑节点数目相等(所有外部节点的黑深度相等)
# 结构
提升:将每个红节点提升,使之与其 parent (必为黑)“等高”;或说,将黑节点与其红孩子视作一个大的节点。如此,将红黑树变换为了 4 阶 B 树((2, 4)-Tree)。
可以验证,提升之后的 B 树中,同一节点不会包含紧邻的红色 key ,有四种情况 - 黑,黑红,红黑,红黑红。
由于 B - 树的平衡性,等价红黑树也是平衡的,高度为,具体地。
黑高度 即位对应的 B - 树高度,B - 树每个节点唯一对应红黑树的黑节点,于是。
# 插入
- 调用 BST 的标准
search;待插入key不存在;search过程中记录了hot。 - 创建红节点,以
hot为parent,黑高度。 - 若 的
parent为红,则双红修正。
# Double Red Issue
插入 后,依次确认其祖先,。若 为红,则需双红修正。
总图:
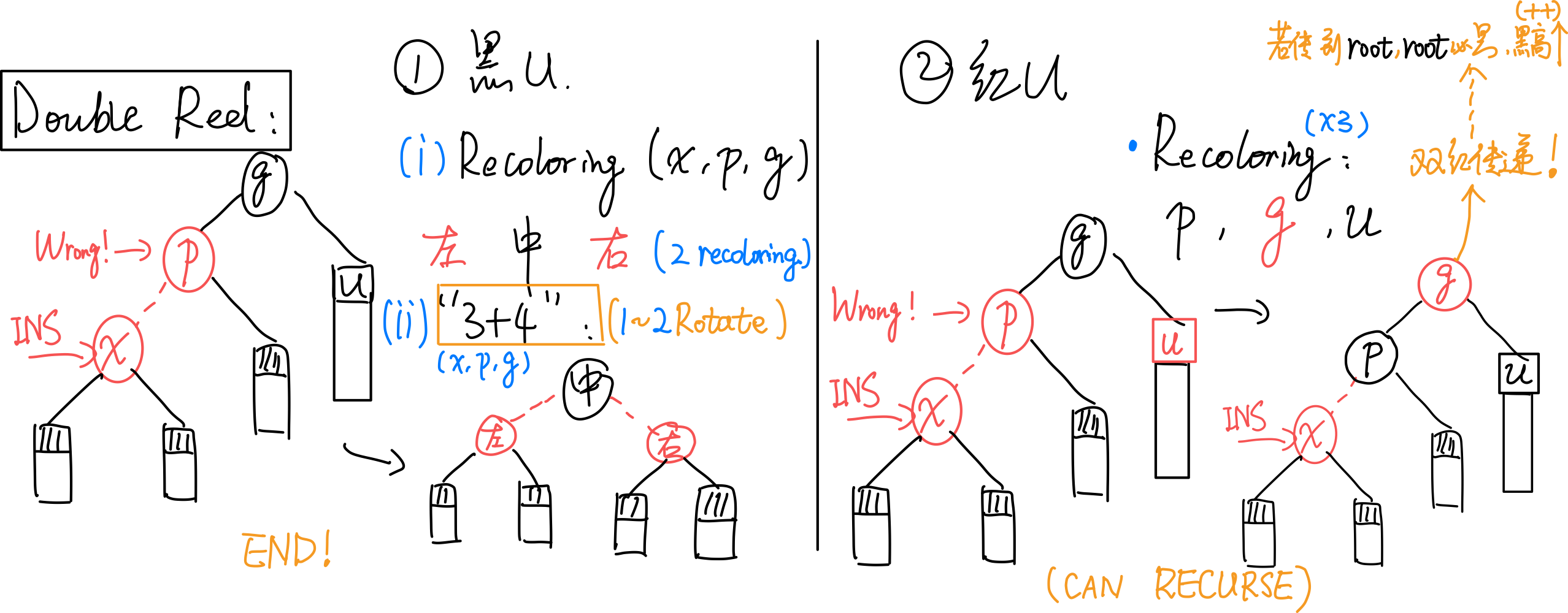
考查 u:
[1] 为黑:
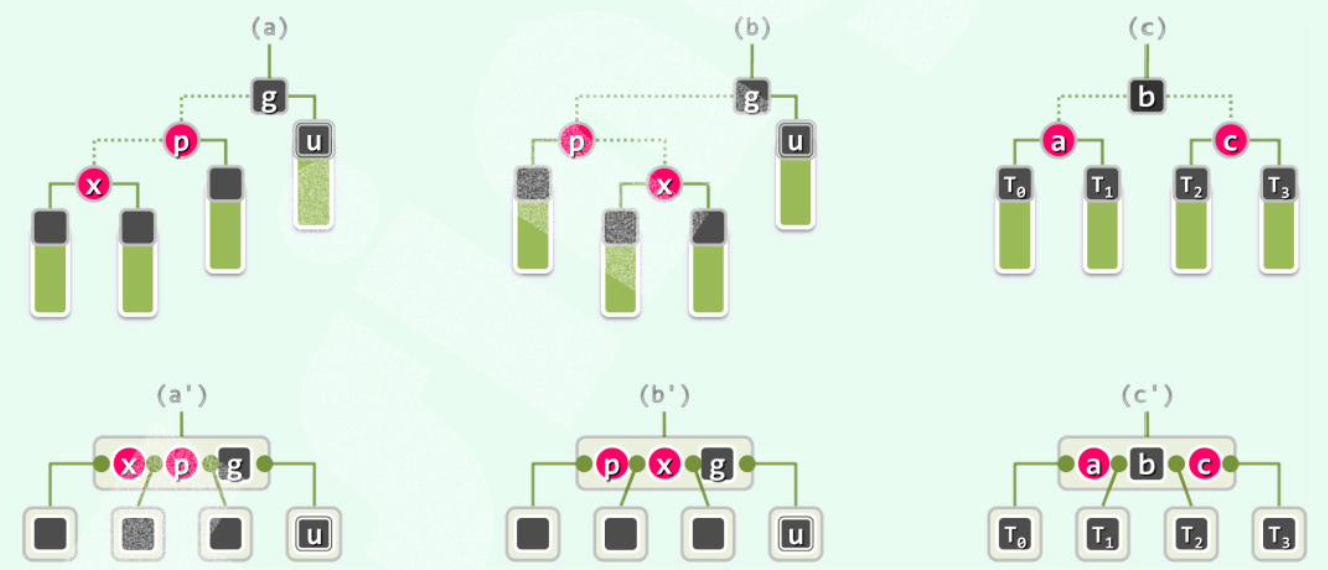
(1)recolor(重新染色):无论顺向(a)还是反向(b),按中序遍历,让,, 中,在 <u> 中间的为黑,两侧的为红 </u>;
(2)用 <u>“3+4 重构”</u > 调整其拓扑结构。
调整完即结束,无缺陷传递。
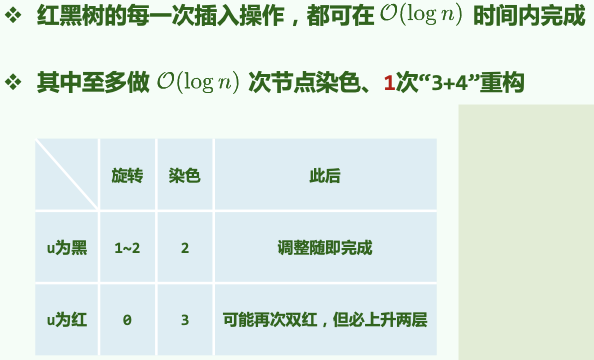
[2] 为红:
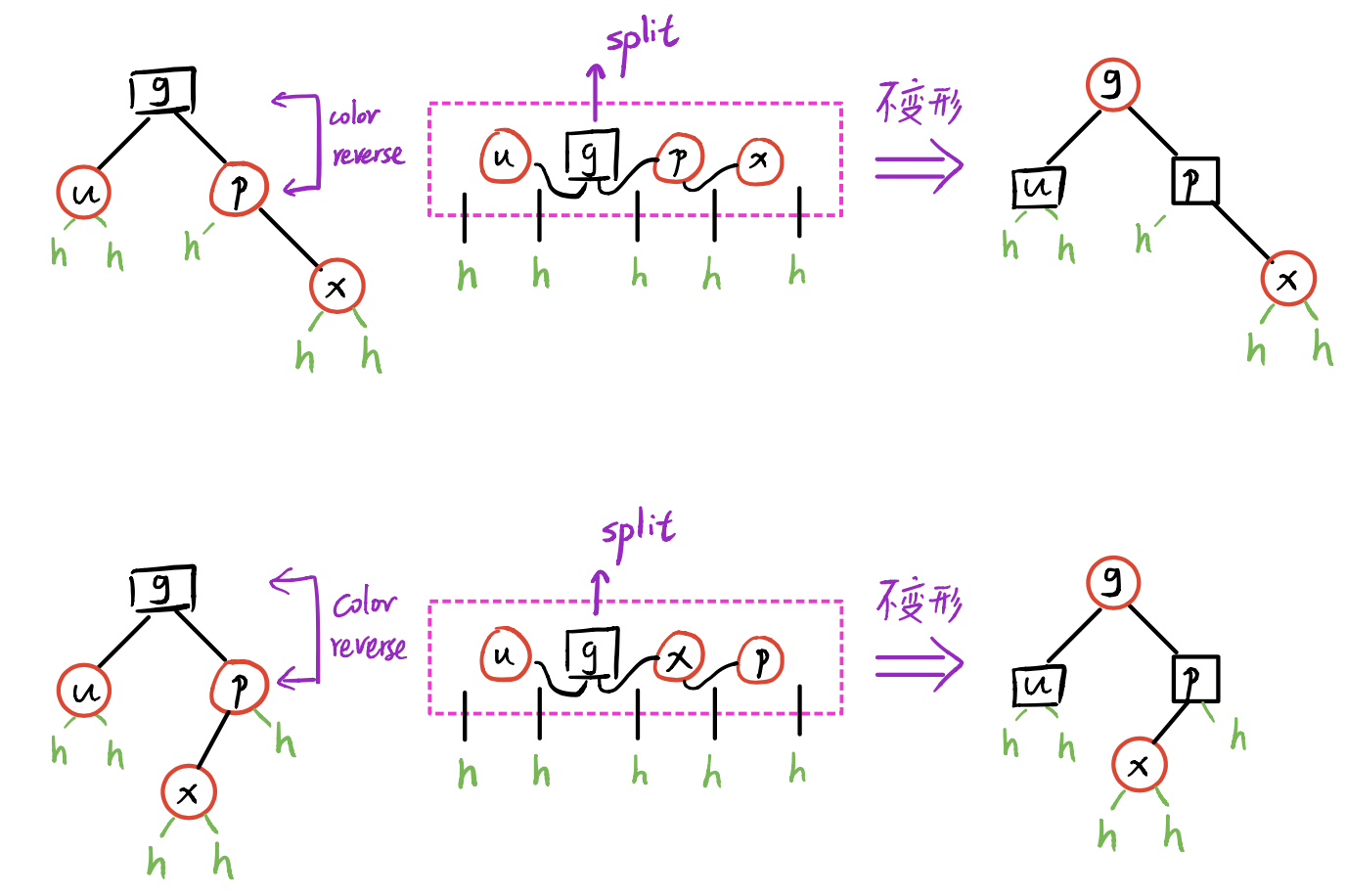
(借助 B 树的理解,即节点发生了上溢。)
recolor:无论是顺向还是反向,均只需:将, 由红转黑(、 黑高度 ++),将 由黑转红。
<u>(拓扑结构不变)</u>
双红传递:由于 的变红,可能导致双红向上传递,因此需要递归地修复。有可能上溯至 root ,但由于规定 root 必为黑,故此处会发生 <u> 全树黑高度增加 </u>。
总结:重染色时间。拓扑结构改变。
# 删除
调用 BST 常规
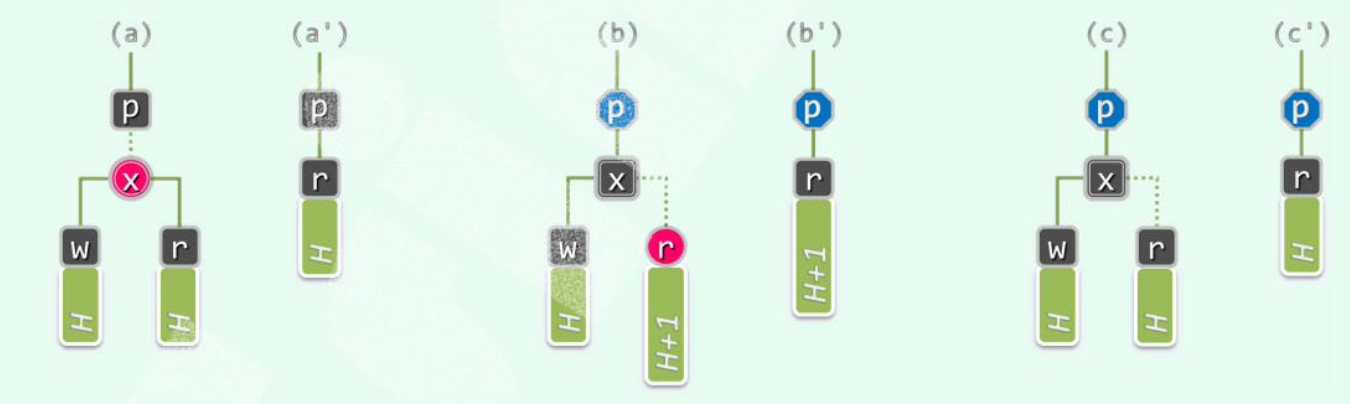
remove算法。实际删除者为。 可能有右孩子,会 “接替”。为红或 为红:
![Screen Shot 2021-01-06 at 12.21.38 PM]()
若 和 同时为黑(c),则需双黑修正。若不是,分情况:
(a) 为红, 为黑,无需调整。
(b) 为黑, 为红, 接替 后变黑。
# Double Black Issue
将会导致全树黑深度不再统一。
总图:
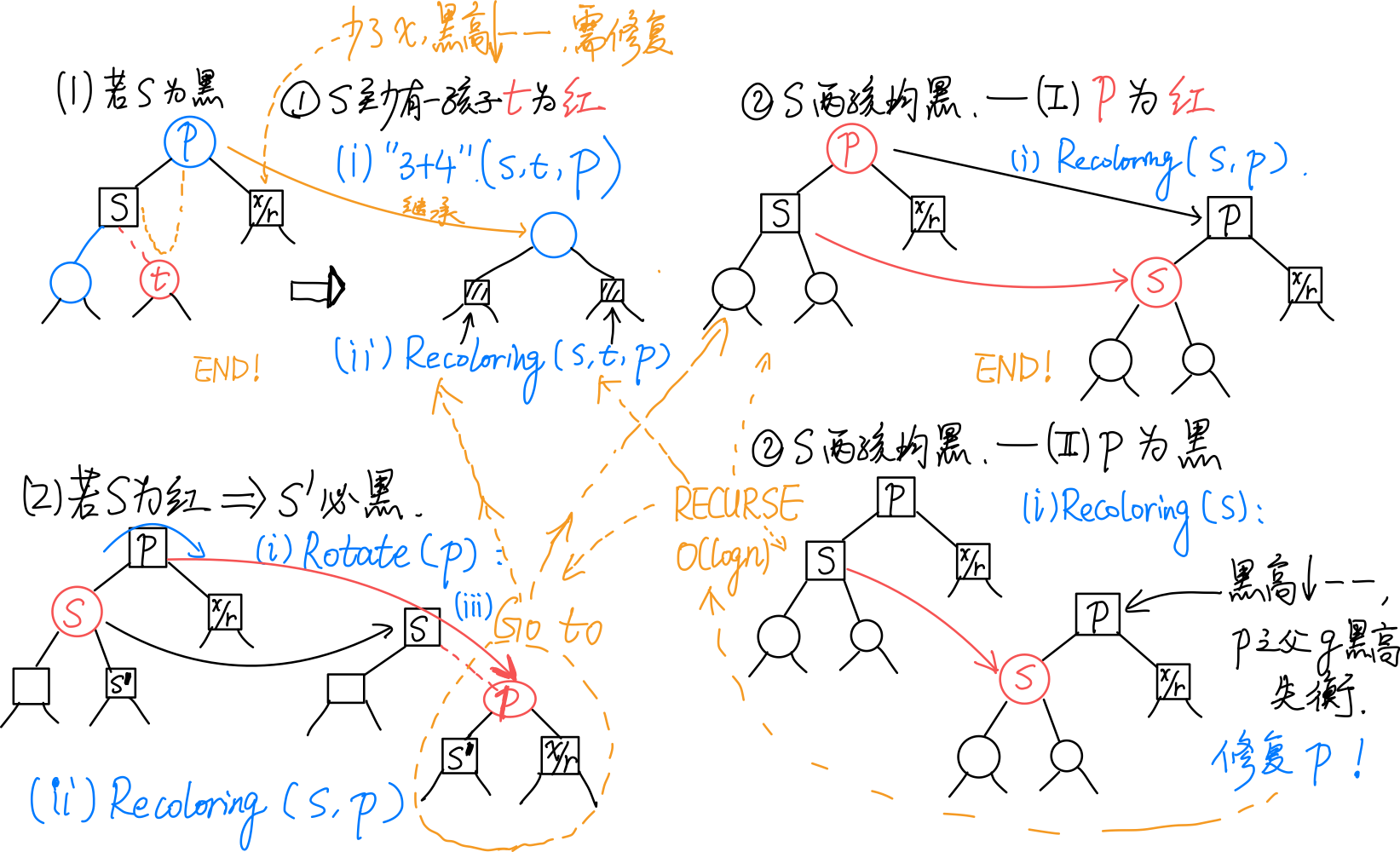
若 和 同时为黑,考查 的兄弟(即 的另一孩子)的颜色及 的孩子的颜色:
[1] 若 为黑:
(1) 至少有一孩子 为红:

(对应 B 树下溢。)
采用 “3+4 重构” 调整拓扑结构,、、 三者中居中者继承 原先的颜色,其余染黑。
调整立即结束,无传递!
(2) 两孩子均为黑:
(i) 为红:
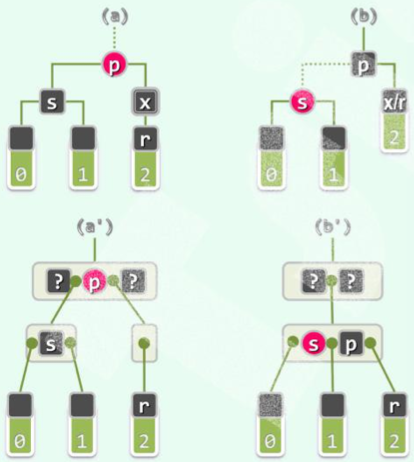
(对应 B 树下溢。)
令 为红, 为黑()。无需调整拓扑结构。
调整立即结束,无传递!
(ii) 为黑:
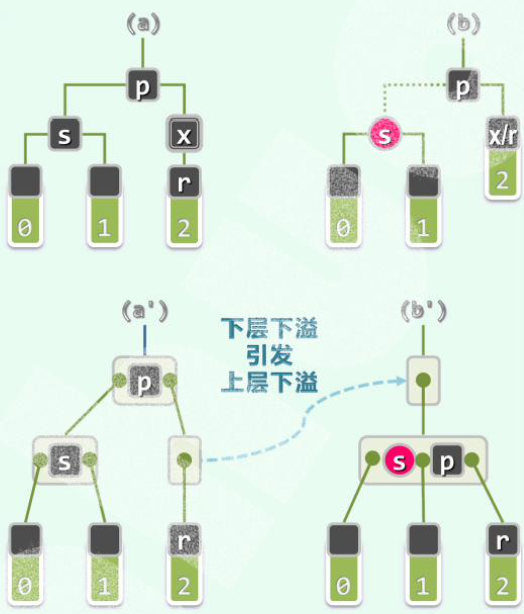
(对应 B 树,下溢引发了上层下溢,需继续递归调整。)
令 为红。
然后以 为根的整棵子树黑高度减。若 有 parent ,则 的黑高度失衡。因此需递归地 <u> 于 和</u> 进行双黑修正。
向上递归。但从红黑树来看拓扑结构不变。
[2] 若 为红:
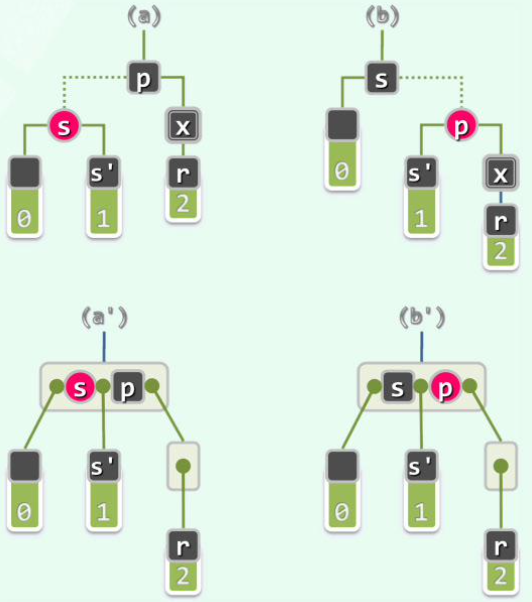
(则 必然是黑的)
此时,观察以 为根的子树: 必为黑,即情况 1;而 为红,因此不会是「情况 [1]-(2)(ii)」。于 处继续递归地双黑修正即可。
递归一层便结束,不会传递!
删除总结:
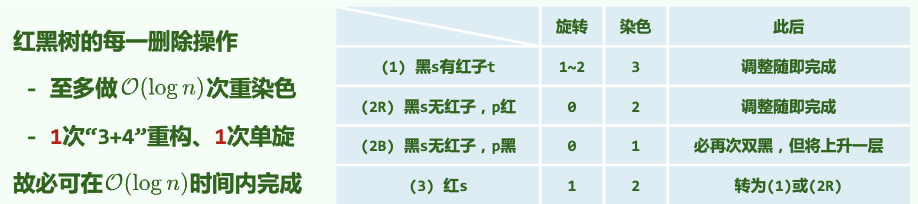
总结:对任何操作,拓扑结构的改变,重染色可能。
# 散列
关键码不再是整数,未必可以定义大小。
装填因子:,装填因子越大,冲突情况越严重。
数据集已知且固定时可以实现完美散列,仅需要 空间,关键码之间互不冲突,查找复杂度。
评价标准与设计原则:
- 确定:同一关键码总是被映射到同一地址。
- 快速:计算。
- 满射:尽可能充分地覆盖整个散列空间。
- 均匀:映射到各位置的概率尽量接近,避免聚集。
基本方法:
除余法(对一个素数取模);
MAD 法(, 为素数且不整除);
数字分析法(抽取几位构成地址);
平方取中(取 的中间若干位);
折叠法(等宽分字段,再求和);
位异或法(等宽分二进制段,连续异或)……
性质:不动点,相关性(相邻关键码也相邻)。
法:将字符串转化为整数,再进行散列运算。
# 闭散列
建议的装填因子: .
闭散列必然对应开放地址法。每个词条都事先约定若干备用的,优先级次逐渐下降。
# Linear Probing
ht[ hash(key) % M ] 被占据 → ht[ (hash(key) + 1) % M ] 。
只要还有空桶,迟早会命中。
# 查找
依次向后找,对应一个查找链。当遇到空桶(且后述 为)时,查找失败。
# lazy tag
删除时,如果仅仅将桶清空,则会造成查找链断裂。为此给每个桶引入,记录这里曾经是否有过元素。
当 为 时,代表这里删除过元素,在查找的时候被视作非空且必不匹配,试探链得以延续。而在插入时依然视为空桶,且插入后若存在标记则删除懒惰标记。
# 重散列
当装填因子增大时冲突概率提升,需要整体搬迁至一个更大的散列表。(装填因子高于,注意这里装填因子的计算要用)
删除的时候懒惰标记过多 () 也需要重散列。
- 将哈希表容量设置为现在已填充项 的四倍。
- 删除原来的懒惰标记,创建新的懒惰标记位图。
- 将旧表中的每个元素转移到新表中。
如果装填因子过小(懒惰标记数目过多),也需要重散列。
# 平方试探
ht[ hash(key) % M ] 被占据 → ht[ (hash(key) + j^2) % M ] ()
优势:试探位置的「间距」以线性速度增长;一旦发生冲突,可以尽快跳离聚集区段。
# 避免无限试探
一种无限循环无法找到空桶的情况(哈希表大小 ; 装填因子 ):

Thm. 若 为素数且装填因子 一定可以找出空桶。
M 若为合数 的可能取值可能小于 。
M 若为素数 的可能取值 = ,且由试探链的前 项取遍(当,,对应 至 的模)。
# 双向平方试探
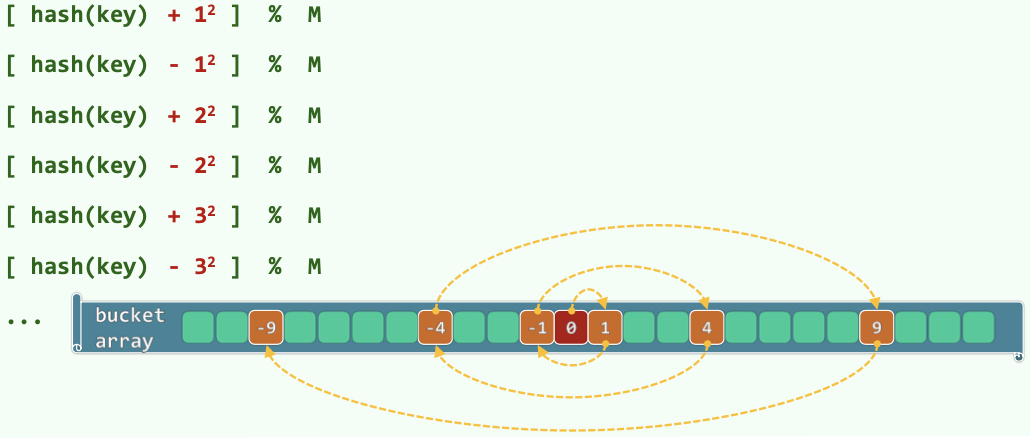
Thm. 表长取形如 的素数,则必然可以保证查找链的前 M 项互异,即正向与反向的查找链除 处无公共的桶。
# 桶排序
空间,时间。如允许重复,每一组同义词各成一个链表,,稳定!
解决问题:最大缝隙。每个桶代表一个区间,需要记录的是这个区间内点的最左和最右值(可能为空)。
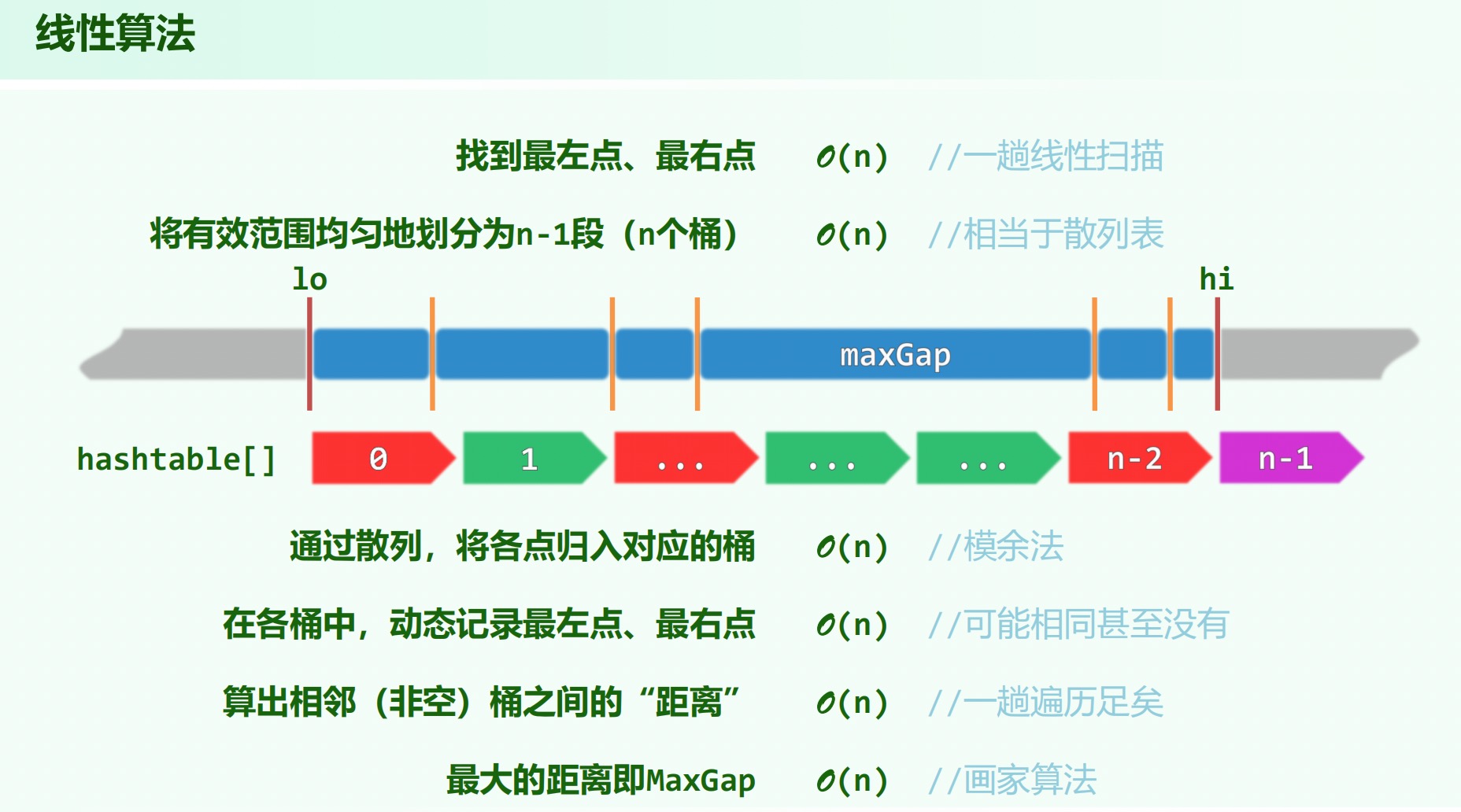
因为 至少跨越两个桶,一趟遍历算出相邻非空桶的距离即可。。
# 基数排序
<u> 低位优先 </u > 的桶排序。前 趟排序后所有词条关于低 位有序。
数据规模为 n,数字位数为 t,每一位的范围为。
复杂度。(一般优于。)稳定!
在常对数密度的整数集上,即考察取自 的 个整数,对数密度为。将所有 个元素转换为 进制形式,于是每个元素转化为 个域,排序时间为。
# 图
邻接矩阵使用二维向量,适用于稠密图,但 空间与边无关,稀疏图造成空间浪费。
邻接表,对于平面图有,近似于。判断边 复杂度达到,如果使用散列才能达到。
# 广度优先搜索
借助队列,类似树的层次遍历。将边分为树边和跨边。复杂度。
BFS (v) 以 v 为根生成一棵 BFS 树,BFS 也能解决最短路径问题,队列中顶点的 差距不超过,由树边相邻顶点 差为 1,跨边则至多相差 1(同一层或相邻两层)。
# 深度优先搜索
时间戳 表示发现时间, 表示访问时间,在发现之后,其所有邻居节点都被发现或访问之后。
使用递归,类似于树的先序遍历,视节点状态若尚未发现则为树边,若已发现但未访问则为被后代指向祖先的后向边,若已经访问(只在有向图中出现)视访问时间戳分为前向边和跨边。
采用邻接表实现复杂度。DFS (v) 以 v 为根生成一棵 DFS 树。
记,则有:
是 的后代当且仅当;
是 的祖先当且仅当;
和 无关当且仅当;
# 拓扑排序
对有向无环图 DAG,将所有顶点排成一个线性序列,使其次序须与原图相容(每一顶点都不会通过边指向前驱)。即对偏序关系 构造全序关系,使所有节点之间满足 和 至少有一个成立。
策略:顺序输出零入度顶点,并删除与其关联边。
策略:逆序输出零出度顶点,对图作 DFS,将访问完毕的顶点压入栈 S,一旦发现后向边则代表出现回路直接退出。之后顺序弹出栈中所有顶点,它们按 逆序排列。
# 优先级搜索
为每个顶点维护一个优先级数,可能随着算法推进而调整。优先级数越大,优先级越低。

前一内循环邻接矩阵,邻接表;后一内循环。若采用优先队列可以优化到 和。
# Dijkstra
单源最短路径。

# Prim
最小支撑树。分成两个割,引入极短跨边。PFS 与 Dijkstra 完全相同,除了 的更新策略。
# Kruskal
维护图的一个森林,初始化包含 棵单节点无边的树;迭代寻找当前最短边,若 的顶点来自森林中不同的树,则在边集中加入该边并将两棵树合并,否则忽略,直到选出 条边。
用并查集维护:初始化 father[i]=i , find(i) = (father[i] == i ? i : find(father[i])) 。
# 优先队列
作为底层数据结构所支持的高效操作,是很多高效算法的基础。
Steap 和 Queap 是插入和删除位置受限的优先队列。
# 完全二叉堆
逻辑上等同于完全二叉树,可以用向量存储,满足。
# 插入
插入在最后,逐层上滤。
。
shift_up(i): // 将第 i 号节点上滤 | |
{ | |
while (i > 0): //i 不是根节点 | |
{ | |
if (data[i] < data[ parent_of[i] ]): | |
break // 已经满足 | |
else: // 父节点比子节点优先级低 | |
swap(data[i], data[ parent_of[i] ]) // 将子节点上移交换 | |
i = parent_of[i] //i 更新 | |
} | |
return i | |
} |
# 删除
删除只有可能在堆顶进行,摘除堆顶并以最后一项替代,之后逐层下滤。
。
shift_down(i): // 将第 i 号节点下滤 | |
{ | |
while (i != proper_parent_at(i)): | |
{ | |
swap(i, proper_parent) | |
i = proper_parent | |
} | |
return i | |
} | |
proper_parent_at(i): | |
// 给出 i 和其两个孩子之间的最大值 | |
// 当三个值相等的时候默认 i 优先为 proper_parent |
数学期望值 - 。
# 批量建堆
蛮力算法:将无规则向量按照下标逐个上滤,最坏情况下,足以全排序。
# Floyd Heapify
。
给定两个堆 和,以及节点,将两个堆的根当作 的左右孩子,再将 下滤,完成合并。
heapify(size n): | |
{ | |
for (i = n / 2 - 1; i >= 0; i--) // 逐下而上 | |
shift_down(i) // 依次下滤所有内部节点 | |
}// 可以理解为子堆的逐层合并 |
# 堆排序
构建完全二叉堆,反复摘除最大元素并归入已排序的后缀( swap(a[0],a[n]) 后下滤)。
# 胜者树
完全二叉树,叶子节点是待排序的元素,每个内部节点都是其孩子中的胜者。
叶子节点需要更新的时候,更新节点和其兄弟一次比较,确定更新是否要向上传递。
空间,因为内部节点都是用节点胜者的标号存储的。
创建复杂度,插入和删除复杂度。
# 败者树
内部节点记录对应比赛的败者,增设一个根的父亲节点代表决赛胜者。败者即被淘汰,在更高层比较的是赢下它两个孩子的两个节点。
败者树重构过程如下:将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。
创建复杂度,插入和删除复杂度。
败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关,而胜者树的重构还与该结点的兄弟结点有关。
# 多叉堆
背景:PFS 中各个顶点组织为优先级队列,更新总体复杂度,取最值总体,总体运行时间,对于稠密图反而不如邻接表的 和。
多()叉堆,依然用向量组织,,,当 不是 的幂不能借助移位运算加速。
堆高降低至,上滤成本降至,但是下滤操作需要比较所有孩子,成本增至 ( 时成本严格高于二叉堆)。
因此 PFS 运行时间将是,当 时总体性能达到最优。
对于稀疏图,因此;对于稠密图,因此。
# 左式堆
目的:在 的时间内实现两个堆的合并( 法为)。
思路:沿着藤作归并,复杂度为藤长。
空节点路径长度:(已经加入所有外部节点)
若 为外部节点,则;否则,
的意义: 到外部节点的最短距离。
左式堆:。
即,对 值,任意内部节点的左孩子不小于右孩子。
倾向于更多的节点分布于左侧分支,然而如图,左子树的高度并不一定不小于右子树。
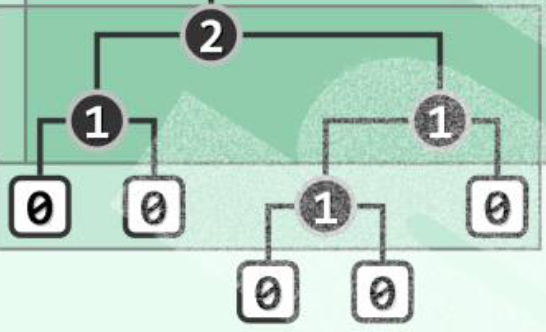
于是有性质:,也等于最右侧通路的长度。。
右侧链的终点是堆中最浅的外部节点。
# 合并
merge(a,b) :
- 通过交换确保,确定 为根,保留。
- 任务变为将 与 合并成新的,依次递归。
- 递归退出后,判断 的左右孩子的 值,若新的 与 不满足 关系,则交换之。
- 维护 的。
# 插入和删除
插入:将新节点单独的树与原节点合并。
删除:删除根,两个字树合并。
# KMP 算法
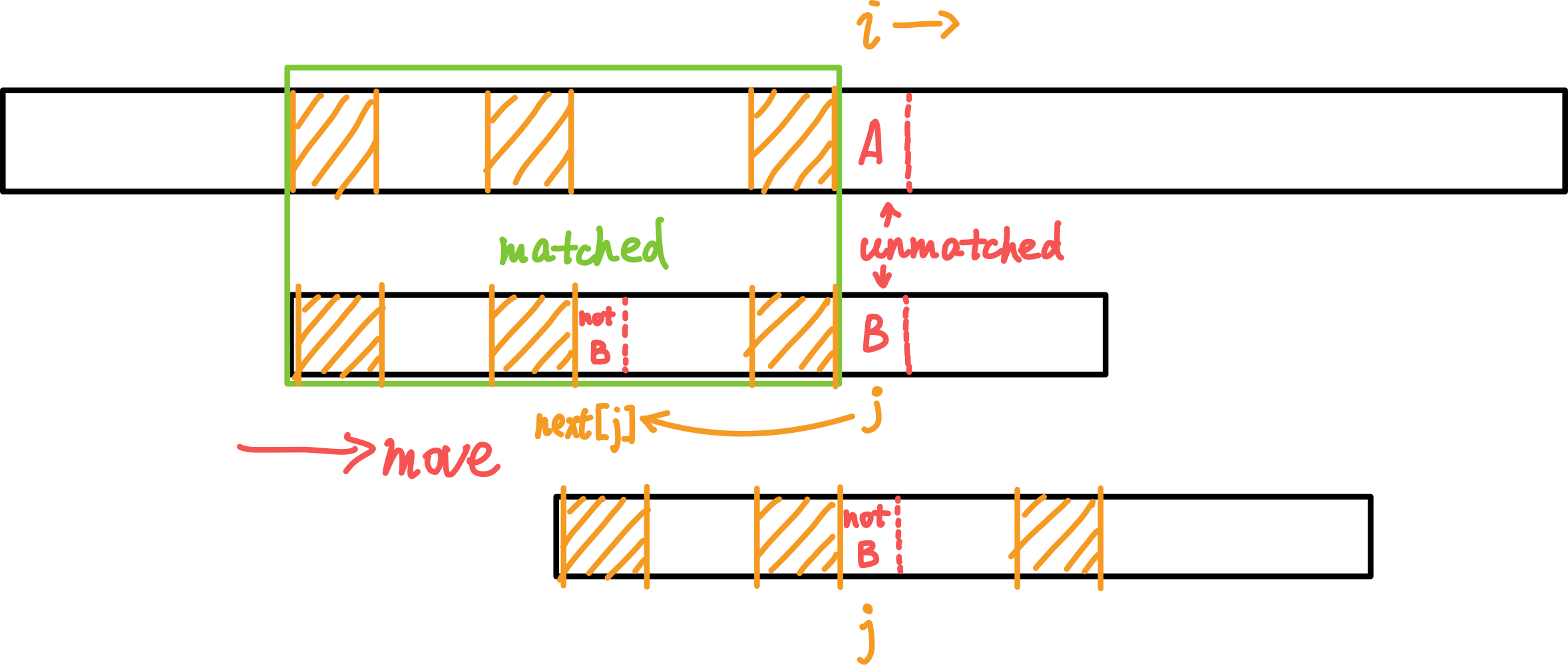
总:。
(上面为一长字符串;下面为需要在上面的串中查找的模式串。黄色阴影区域表示相同的子串。)
当失败时, j (向前)跳转至 next[j] 继续尝试匹配。而 i 始终向后,保证了复杂度为。
若匹配成功,会有 j == m 跳出循环。返回值 i - j (i - m) 就是匹配上的模式串在主串中的起始位置。
扫描一趟。
# Next 表
。
表示模式 的 区间内,最大公共真前缀后缀的长度,即需要保证。
。
,代表若在某一轮中首对字符即失配,则应将模式串直接右移一个字符。
若,当 时有,否则。
若, 的候选者应当依次是,,即反复用 替换,直到能够满足 或。
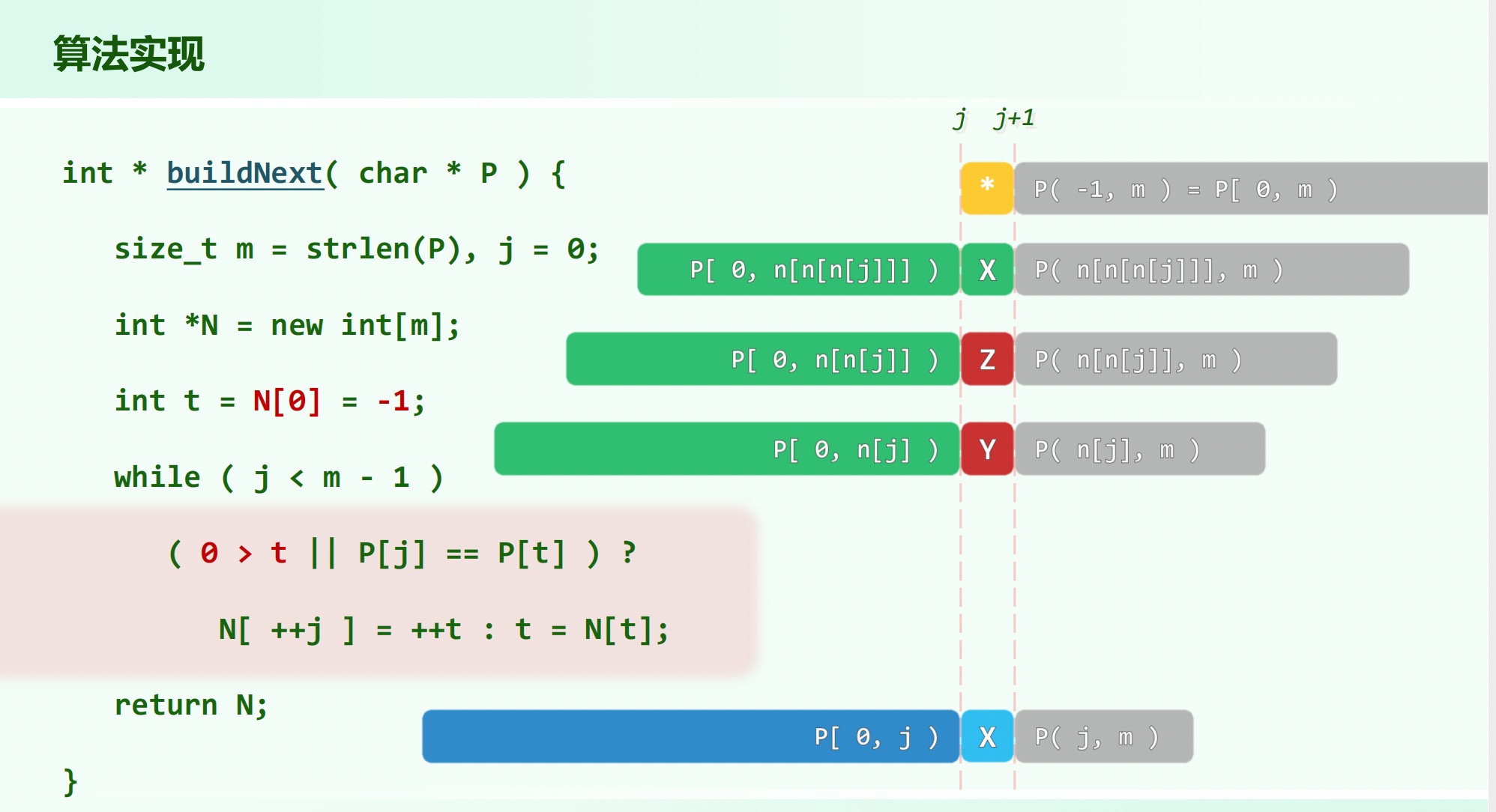
# 分摊分析

# 再优化
表的构造附加条件。
即在匹配时 仅仅在 的时候被赋值为,否则赋值为。
吸取经验(成功的匹配)与教训(失败的匹配)。
# BM 算法:BC 策略
复杂度比较
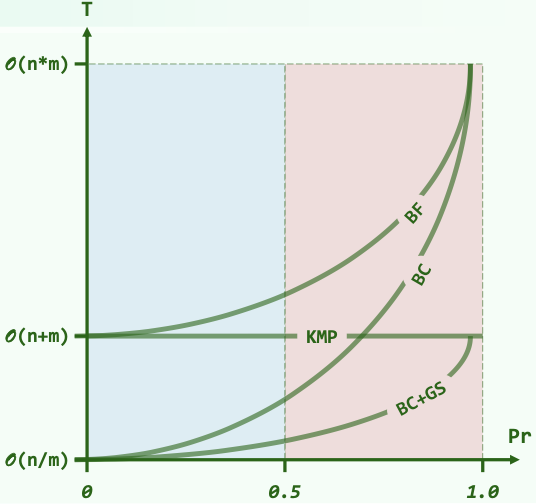
()
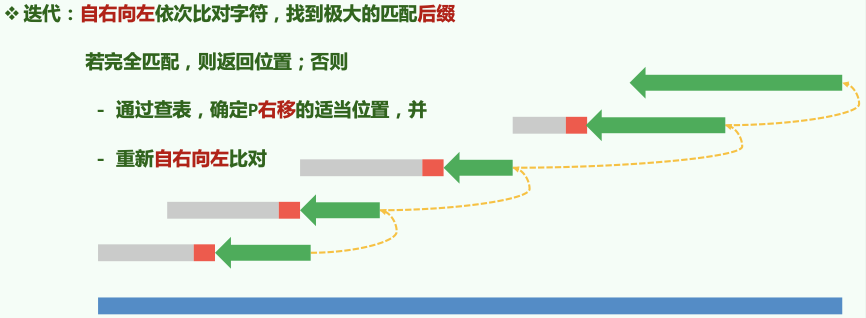
# Bad Character Shift
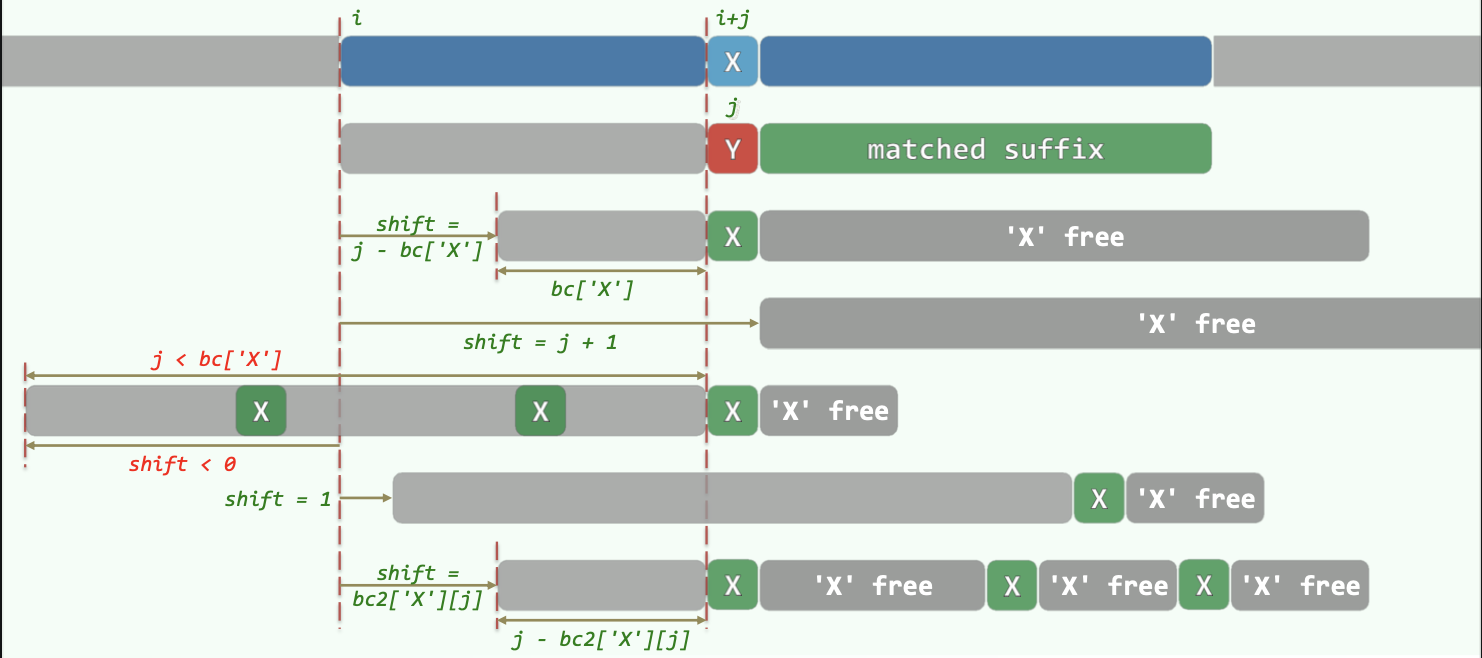
若某处(主串字符为 X,模式串为 Y)匹配失败,则用 BC 表找到模式串 P 中最后一个 X 字符出现的位置,将这个位置对准主串进行匹配。
如果 P 中最后一个 X 出现的位置在 Y 之前,则相当于 P 右移。
若 P 中最后一个 X 出现的位置在 Y 之后,其实无需也不能左移。(保持 P 一直右移的单调性。)此时直接将 P 右移一个位置即可。
# BC 表
- BC 表长度为字符集的大小。
- BC 表初始化为每一项为 - 1,对应字符未出现在 P 中。
- 从左向右扫描 P,令
BC[ P[i] ] = i即可记录每个字符在 P 中出现的最后位置。
# 性能
最好情况,最差情况。单次匹配概率越小,性能优势越明显。
# Karp-Rabin 算法
凡物皆数:长度有限的字符串,都可以视作 进制的自然数( 为字母表);长度无限的字符串,都可以视作 内的 进制小数。
一般地,对字符编号,每个字符串对应于一个 进制自然数(指纹), 在 中出现仅当 中某一子串对应的自然数与 相等。
但如果 很大,单个 位字长的存储器无法单独存储,从而导致指纹的计算和判等需要的时间完成,总体时间达到。
散列表压缩指纹:设计适当的散列函数降低冲突概率,使得 值相等即可判断相等。
每次计算文本串中长度为 的子串指纹时可以在 时间切换到下一指纹。
# 快速排序
# 轴点
以轴点为界,左侧 / 右侧的元素均不比他更大 / 更小。快速排序就是将所有元素逐个转换为轴点的过程。
QuickSort(lo, hi):
{ // [lo, hi)
if (hi - lo >= 2)
{
mi = partition(lo, hi - 1)
QuickSort(lo, mi)
QuickSort(mi + 1, hi)
}
}
# Partition
随机选择一点作为(轴点),让其就位。
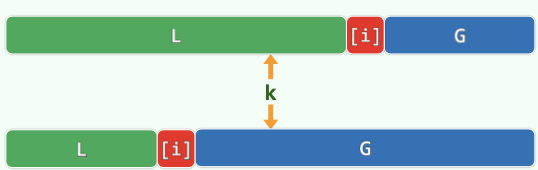
版的 Partition 。始终有。
Partition(lo, hi): | |
{ // [lo, hi] | |
swap(data[lo], data[randint(lo, hi)]) | |
pivot = data[lo] // 随机选取轴点 | |
while (lo < hi) | |
{ | |
while (lo < hi && pivot <= data[hi]) //pivot 小于 G 区间左边待拓展节点时 | |
hi-- // 向左拓展 G | |
data[lo] = data[hi] // 把 G 区间左边小于 pivot 的数放在 L 右端(相当于拓展 L) | |
while (lo < hi && data[lo] <= pivot) //pivot 大于 L 区间右边待拓展节点时 | |
lo++ // 向右拓展 L | |
data[hi] = data[lo] // 把 L 区间右边大于 pivot 的数放在 G 左端(相当于拓展 G) | |
} // 继续循环拓展 G、L | |
// assert: lo == hi | |
data[lo] = pivot | |
return lo | |
} |
不稳定!
最坏情况下每次划分均偏侧,递归深度达到,时间复杂度。采用随机选取,三者取中的策略只能降低最坏情况的概率而无法杜绝。
# 递归深度
准居中: 落在宽度为 的居中区间。
每一条递归路径上最多出现 个准居中的轴点。

# 比较次数
# 递推分析
假设待排序的元素服从独立均匀随机分布。于是 partition() 算法经过 次比较和至多 次移动后,对规模为 的向量划分结果有 种可能,即左侧子序列长度为 到,每种情况概率为。

# 处理重复元素
版:重复元素总使 增加, 减少。
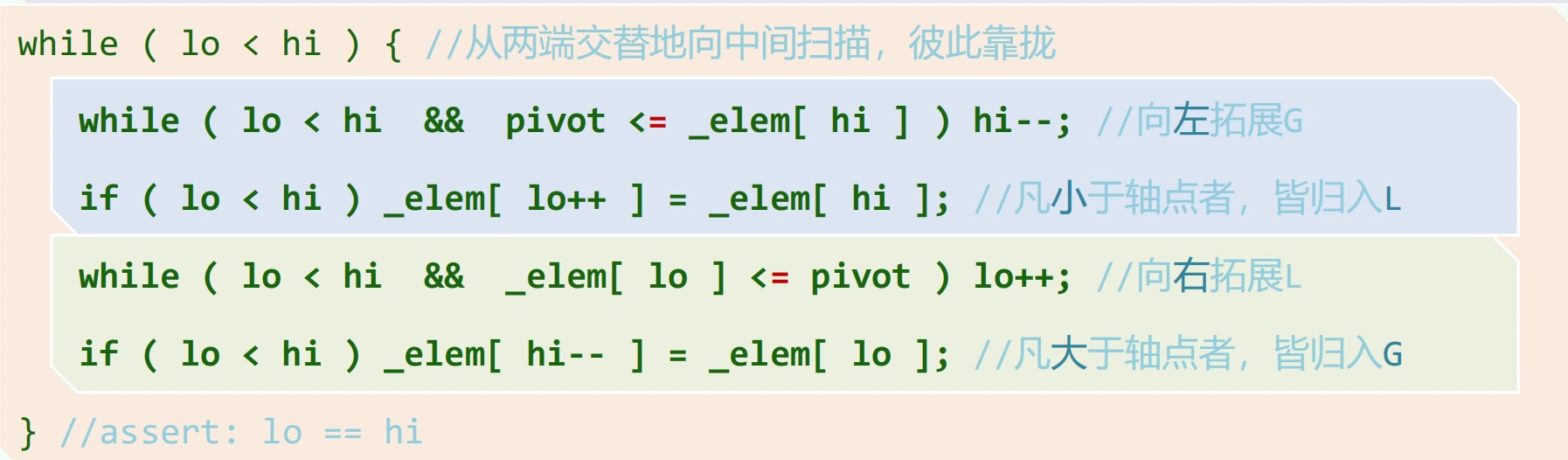
版:改为不大于和不小于。

版:同上。

处理重复元素时将轴点最后能安放在中点处,由 版勤于拓展,懒于交换改为勤于交换,懒于拓展。
交换操作有所增加,更不稳定!
# LGU 算法
。
满足。

逐个考察,小于轴点则通过交换扩展 区域,同时 区域长度不变滚动向前;否则扩展 区域。最后 区域被消耗完毕,轴点归位。
# 选取问题
# 众数
在无序向量中,若有一半以上元素同为,则称之为众数。
众数若存在则必为中位数!只要能找出中位数则不难验证它是否是众数(扫描记录出现次数)。
一个重要事实:设 为向量 中长度为 的前缀,若元素 在 中恰好出现 次,则 有众数仅当后缀 有众数,且 的众数就是 的众数。
仅考虑 含有众数的情况:若 的众数就是,显然成立;否则若 的众数为,则在剪除前缀之后 减少的数目也不会多于非众数减少的数目,二者差距在后缀 中也不会缩小。
算法:
template <typename T> T majEleCandidate ( Vector<T> A ) { // 选出具备必要条件的众数候选者 | |
T maj; // 众数候选者 | |
// 线性扫描:借助计数器 c,记录 maj 与其它元素的数量差额 | |
for ( int c = 0, i = 0; i < A.size(); i++ ) | |
if ( 0 == c ) { // 每当 c 归零,都意味着此时的前缀 P 可以剪除 | |
maj = A[i]; c = 1; // 众数候选者改为新的当前元素 | |
} else // 否则 | |
maj == A[i] ? c++ : c--; // 相应地更新差额计数器 | |
return maj; // 至此,原向量的众数若存在,则只能是 maj —— 尽管反之不然 | |
} |
# 归并向量的中位数
对于等长子向量,,左右两图为偶数和奇数的情况:

任意长的向量:递归基,直接求解;若相差悬殊则长者的两侧可以直接删除(),否则:

# Quick Selection
几个尝试:
- 全部组织成小顶堆。
- 任选 个元素组织成大顶堆,在 区间内的元素依次入堆后删除堆内最大值,之后弹出最大值即可。
- 任意划分为 和 的子集,分别组织为大、小顶堆,交换并下滤两个堆顶元素,直到大顶堆根小于等于小顶堆的根,返回小顶堆的根。。
QuickSelect(lo, hi, k): | |
{ | |
while (lo < hi) | |
{ | |
// 准备工作,为快排中的 quick partition 准备 | |
swap(data[lo], data[randint(lo, hi)]) | |
i = lo, j = hi, pivot = data[lo] | |
// 对于 [i, j] 区间执行 quick partition 操作找出轴点并分割 | |
// 退出时必有 i == j; data [i] 就是轴点 | |
// 逐步缩小 [lo, hi] 到含有 k_th element 的范围 | |
if (k <= i) | |
hi = i - 1 | |
if (i <= k) | |
lo = i + 1 | |
} | |
} |
复杂度归纳证明:

但在最坏情况下仍为。
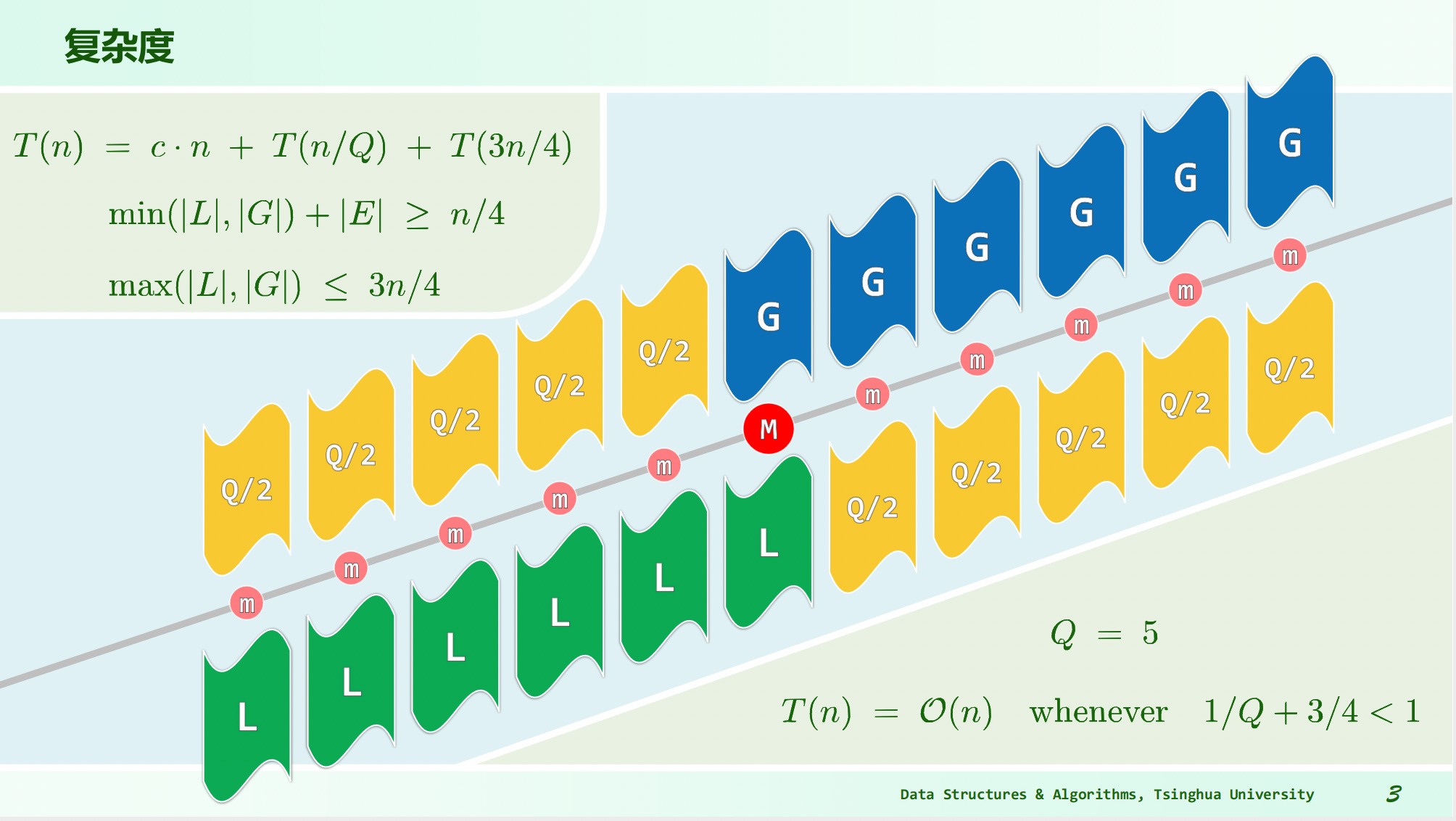
# Linear Select
- 取一个小的常数。
- 递归基:序列规模小于 的时候直接用蛮力算法排序求中位数。
- 将 均匀地划分为 个子序列,分别排序计算中位数,并将这些中位数组成一个序列。
- 通过递归调用计算出中位数序列的中位数,记作。
- 根据相对于 的大小,将 A 中元素分为三个子集:(小于),(等于),(大于)。
- 如果 则递归调用求解 L 的第 小元素;否则若 直接返回 M;否则递归调用求解 G 的第 小元素。
复杂度:记作,第 3 步,第 4 步,第 6 步?
至少有一半的子序列中,有半数的元素不小于;同理也有至少 的元素不大于。因此递归后的子集大小不超过,为。